题目内容
已知f(x)是定义在区间[-1,1]上的奇函数,且f(1)=1,若m,n∈[-1,1],m+n≠0时,有
>0.
(1)判断f(x)的单调性,并证明;
(2)若f(x)≤t2-2at+1对所有x∈[-1,1],a∈[-1,1]恒成立,求实数t的取值范围.
| f(m)+f(n) |
| m+n |
(1)判断f(x)的单调性,并证明;
(2)若f(x)≤t2-2at+1对所有x∈[-1,1],a∈[-1,1]恒成立,求实数t的取值范围.
考点:函数奇偶性的性质,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)利用已知与增函数的定义即可得出;
(2)由于f(x)为增函数,可得f(x)的最大值为f(1)=1.f(x)≤t2-2at+1对a∈[-1,1],x∈[-1,1]恒成立?t2-2at+1≥1对任意a∈[-1,1]恒成立?t2-2at≥0对任意a∈[-1,1]恒成立.看作a的一次函数,即可得出.
(2)由于f(x)为增函数,可得f(x)的最大值为f(1)=1.f(x)≤t2-2at+1对a∈[-1,1],x∈[-1,1]恒成立?t2-2at+1≥1对任意a∈[-1,1]恒成立?t2-2at≥0对任意a∈[-1,1]恒成立.看作a的一次函数,即可得出.
解答:
解:(1)任取x1、x2∈[-1,1],且x2>x1,则
f(x2)-f(x1)=f(x2)+f(-x1)=
•(x2-x1)>0,
∴f(x2)>f(x1),∴f(x)是增函数.
(2)由于f(x)为增函数,∴f(x)的最大值为f(1)=1,
∴f(x)≤t2-2at+1对a∈[-1,1]、x∈[-1,1]恒成立?t2-2at+1≥1对任意a∈[-1,1]恒成立?t2-2at≥0对任意a∈[-1,1]恒成立.
把y=t2-2at看作a的函数,
由a∈[-1,1]知其图象是一条线段,
∴t2-2at≥0对任意a∈[-1,1]恒成立
?
,解得
解得:t≤-2,或t=0,或t≥2.
f(x2)-f(x1)=f(x2)+f(-x1)=
| f(x2)+f(-x1) |
| x2+(-x1) |
∴f(x2)>f(x1),∴f(x)是增函数.
(2)由于f(x)为增函数,∴f(x)的最大值为f(1)=1,
∴f(x)≤t2-2at+1对a∈[-1,1]、x∈[-1,1]恒成立?t2-2at+1≥1对任意a∈[-1,1]恒成立?t2-2at≥0对任意a∈[-1,1]恒成立.
把y=t2-2at看作a的函数,
由a∈[-1,1]知其图象是一条线段,
∴t2-2at≥0对任意a∈[-1,1]恒成立
?
|
|
解得:t≤-2,或t=0,或t≥2.
点评:本题考查了抽象函数的单调性、恒成立问题的等价转化方法、一次函数的单调性,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
复数
的虚部为( )
| 1+2i |
| 2+i |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知A(-2,0),B(0,2),实数k是常数,M,N是圆x2+y2+kx=0上两个不同点,且M,N关于直线x-y-1=0对称,若P是圆x2+y2+kx=0上的动点,则△PAB面积的最大值是( )
A、3-
| ||
| B、4 | ||
C、3+
| ||
| D、6 |
某几何体的三视图如图所示,当a+b取最大值时,这个几何体的体积为( )
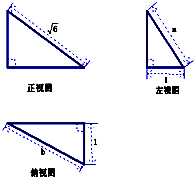

A、
| ||
B、
| ||
C、
| ||
D、
|
点(-1,0)到直线12x+5y-1=0的距离是( )
A、
| ||
| B、1 | ||
C、
| ||
| D、13 |
已知圆上的一段弧长等于该圆的内接正方形的边长,则这段弧所对的圆周角的弧度数为( )
A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
如图所示是计算某年级500名学生期末考试(满分为100分)及格率q的程序框图,则图中空白框内应填入( )
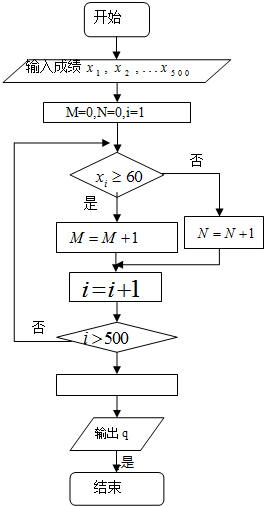

A、q=
| ||
B、q=
| ||
C、q=
| ||
D、q=
|