题目内容
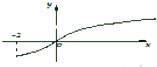 已知f(x)的定义域为[-2,+∞),部分对应值如下表,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图,若f(x)<1,则x的范围为
已知f(x)的定义域为[-2,+∞),部分对应值如下表,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图,若f(x)<1,则x的范围为| x | -2 | 0 | 4 |
| f(x) | 1 | -1 | 1 |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:通过读图得出函数f(x)的单调区间,从而求出函数的最小值,再通过表格求出x的范围.
解答:
解:由图象得:在区间[-2,0)上,f′(x)<0,在区间(0,+∞)上,f′(x)>0,
∴函数f(x)在[-2,0)递减,在(0,+∞)递增,
∴f(x)min=f(0)=-1,而f(-2)=1,f(4)=1,
∴若f(x)<1,只需-2<x<4即可,
故答案为:(-2,4).
∴函数f(x)在[-2,0)递减,在(0,+∞)递增,
∴f(x)min=f(0)=-1,而f(-2)=1,f(4)=1,
∴若f(x)<1,只需-2<x<4即可,
故答案为:(-2,4).
点评:本题考查了函数的单调性,函数的最值问题,考查导数的应用,考查数形结合思想,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设函数f(x)是定义在R上的奇函数,若f(-2)>0,f(2)=4-
,则a的取值范围是( )
| 7 |
| a+1 |
| A、a<0.75 |
| B、a<0.75且a≠-1 |
| C、a>0.75或a<-1 |
| D、-1<a<0.75 |
若正实数x,y满足x+y+
+
=5,则x+y的最大值是( )
| 1 |
| x |
| 1 |
| y |
| A、2 | B、3 | C、4 | D、5 |
复数
的虚部为( )
| 1+2i |
| 2+i |
A、
| ||
B、
| ||
C、
| ||
D、
|