题目内容

当点（x，y）在直线x+3y=2上移动时，u=3x+27y+1的最小值是（　　）
A、7
B、3
39
C、1+2
2
D、6
考点：基本不等式
专题：函数的性质及应用,不等式的解法及应用
分析：把27y化为33y，然后直接利用基本不等式求最值．
解答： 解：点（x，y）在直线x+3y=2上移动，
由u=3x+27y+1=3x+33y+1，
∵3x＞0，33y＞0，
∴3x+33y+1≥2
3x•33y
+1=2
3x+3y
+1
=2
32
+1
=7．
当且仅当3x=33y，即：x=3y=1时等号成立．
故选：A．
点评：本题考查了基本不等式去最值，利用基本不等式求最值一定要注意“一正、二定、三相等”，是基础题．
练习册系列答案
相关题目
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0），离心率为
3
2
，两焦点分别为F1、F2，过F1的直线交椭圆C于M，N两点，且△F2MN的周长为8．
（1）求椭圆C的方程；
（2）过点P（m，0）作圆x2+y2=1的切线l交椭圆C于A，B两点，求弦长|AB|的最大值．
下列命题中为真命题的是（　　）
A、第一象限的角一定是锐角
B、终边相同的角一定相等
C、相等的角，终边一定相同
D、小于90°的角一定是锐角
当-
π
3
≤x≤
π
3
时，函数y=sin x+
3
cos x的最大值和最小值分别为（　　）
A、1，-1
B、1，-
1
2
C、2，
3
D、2，0
已知f（x）=x2+bx+c为偶函数，曲线y=f（x）过点（2，5），g（x）=（x+a）f（x），g（x）的导函数为g′（x）
（Ⅰ）若曲线y=g（x）有斜率为0的切线，求实数a的取值范围；
（Ⅱ）若g′（-1）=0，求y=g（x）的单调区间．
若i为虚数单位，则-i+
1-i
1+i
=（　　）
A、-2i
B、0
C、
1
2
i
D、2i
已知O为坐标原点，
OA
=（2cos2x，1），
OB
=（1，
3
sin2x+a）（x∈R，a∈R，a是常数），若y=
OA
•
OB
．
（Ⅰ）求y关于x的函数解析式f（x）；
（Ⅱ）若x∈[0，
π
2
]时，f（x）的最大值为2，求a的值并指出f（x）的单调区间．
某几何体的三视图如图所示，当a+b取最大值时，这个几何体的体积为（　　）
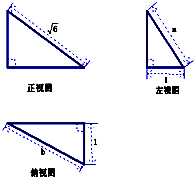
A、
1
6
B、
1
3
C、
2
3
D、
1
2
已知0＜a＜b，且a+b=1，则下列不等式①log2a＞-1；②log2a+log2b＞-2；③log2（b-a）＜0；④log2（
b
a
+
a
b
）＞1，其中一定成立的不等式的序号是（　　）
A、①②B、②③C、③④D、①④

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网