题目内容
如果曲线y=x2与y=-x3在x=x0处的切线互相垂直,则x0的值为 .
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:求导数,确定切线的斜率,利用曲线y=x2与y=-x3在x=x0处的切线互相垂直,建立方程,即可求x0的值.
解答:
解:由题意,y′=2x,k1=2x0;
y′=-3x2,k2=-3x02.
∵曲线y=x2与y=-x3在x=x0处的切线互相垂直,
∴k1k2=-1,
即6x03=1,x0=
.
故答案为:
.
y′=-3x2,k2=-3x02.
∵曲线y=x2与y=-x3在x=x0处的切线互相垂直,
∴k1k2=-1,
即6x03=1,x0=
| |||
| 6 |
故答案为:
| |||
| 6 |
点评:本题考查导数的几何意义,考查两条直线垂直位置关系,考查学生的计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
点(-1,0)到直线12x+5y-1=0的距离是( )
A、
| ||
| B、1 | ||
C、
| ||
| D、13 |
已知圆上的一段弧长等于该圆的内接正方形的边长,则这段弧所对的圆周角的弧度数为( )
A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
已知0<a<b,且a+b=1,则下列不等式①log2a>-1;②log2a+log2b>-2;③log2(b-a)<0;④log2(
+
)>1,其中一定成立的不等式的序号是( )
| b |
| a |
| a |
| b |
| A、①② | B、②③ | C、③④ | D、①④ |
如图所示是计算某年级500名学生期末考试(满分为100分)及格率q的程序框图,则图中空白框内应填入( )
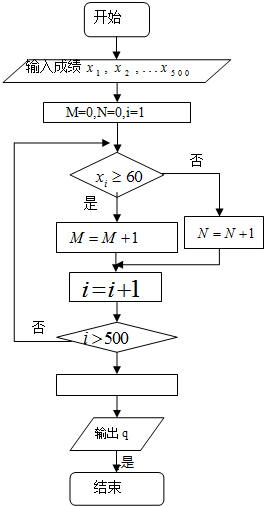

A、q=
| ||
B、q=
| ||
C、q=
| ||
D、q=
|