题目内容
8.已知0<α<$\frac{π}{2}$,且cos($\frac{π}{2}+α$)=$-\frac{\sqrt{2}}{2}$,则sinα=$\frac{\sqrt{2}}{2}$.分析 由条件利用诱导公式求得sinα的值.
解答 解:∵0<α<$\frac{π}{2}$,且cos($\frac{π}{2}+α$)=-sinα=$-\frac{\sqrt{2}}{2}$,则sinα=$\frac{\sqrt{2}}{2}$,
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题主要考查应用诱导公式化简三角函数式,要特别注意符号的选取,这是解题的易错点,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.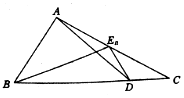 如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N+)为边AC的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )
如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N+)为边AC的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )
 如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N+)为边AC的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )
如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N+)为边AC的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )| A. | 3•2n-1-2 | B. | 2n-1 | C. | 3n-2 | D. | 2•3n-1-1 |
19.已知集合$A=\{x|{x^2}-2x>0\},B=\{x|-\sqrt{5}<x<\sqrt{5}\}$,则( )
| A. | A⊆B | B. | B⊆A | C. | A∪B=R | D. | A∩B=∅ |
16.二项式${({x^2}-\frac{1}{{\sqrt{x}}})^{10}}$的展开式的二项式系数和为( )
| A. | 1 | B. | -1 | C. | 210 | D. | 0 |
3.下列说法正确的是( )
| A. | 三角形的内角是第一象限角或第二象限角 | |
| B. | 第一象限的角是锐角 | |
| C. | 第二象限的角比第一象限的角大 | |
| D. | 角α是第四象限角的充要条件是$2kπ-\frac{π}{2}<α<2kπ(k∈z)$ |
20.若f(x)=2xf'(1)+x2,则f'(0)等于( )
| A. | -2 | B. | 4 | C. | 2 | D. | -4 |