题目内容
20．已知函数f（x）=x+xlnx，若k∈Z，且k（x-1）＜f（x）对任意的x＞1恒成立，则k的最大值为（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
分析 将问题转化为k＜$\frac{xlnx+x}{x-1}$在x＞1上恒成立，令h（x）=$\frac{xlnx+x}{x-1}$，求出最小值即可．
解答 解：由k（x-1）＜f（x）对任意的x＞1恒成立，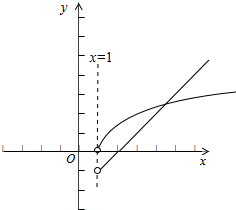
得：k＜$\frac{xlnx+x}{x-1}$，（x＞1），
令h（x）=$\frac{xlnx+x}{x-1}$，（x＞1），则h′（x）=$\frac{x-lnx-2}{（x-1）^{2}}$，
令g（x）=x-lnx-2=0，得：x-2=lnx，
画出函数y=x-2，y=lnx的图象，如图示：
∴g（x）存在唯一的零点，
又g（3）=1-ln3＜0，g（4）=2-ln4=2（1-ln2）＞0，
∴零点属于（3，4）；
∴h（x）在（1，x0）递减，在（x0，+∞）递增，
而3＜h（3）=$\frac{3ln3+3}{2}$＜4，$\frac{8}{3}$＜h（4）=$\frac{4ln4+4}{3}$＜4，
∴h（x0）＜4，k∈Z，
∴k的最大值是3．
故选：B．
点评 本题考查了函数的零点问题，考查了函数恒成立问题，是一道中档题．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
相关题目
15．甲、乙、丙3名学生排成一排，其中甲、乙两人站在一起的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{2}$ |
12．
为了普及环保知识，增强环保意识，某大学随机抽取30名学生参加环保知识测试，得分（十分制）如图所示，假设得分值的中位数为M1，众数为M2，平均值为$\overline x$，则（ ）
为了普及环保知识，增强环保意识，某大学随机抽取30名学生参加环保知识测试，得分（十分制）如图所示，假设得分值的中位数为M1，众数为M2，平均值为$\overline x$，则（ ）| A． | M1=M2=$\overline x$ | B． | M1=M2＜$\overline x$ | C． | M1＜M2＜$\overline x$ | D． | M2＜M1＜$\overline x$ |
9．在△ABC中，B=30°，AB=$\sqrt{3}$，AC=1，则△ABC的面积是（ ）
| A． | $\frac{\sqrt{3}}{4}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\sqrt{3}$或$\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{3}}{2}$或$\frac{\sqrt{3}}{4}$ |
10．y=2cos（$\frac{π}{4}$-2x）的单调减区间是（ ）
| A． | [kπ+$\frac{π}{8}$，kπ+$\frac{5}{8}$π]（k∈Z） | B． | [-$\frac{3}{8}$π+kπ，$\frac{π}{8}$+kπ]（k∈Z） | ||
| C． | [$\frac{π}{8}$+2kπ，$\frac{5π}{8}$+2kπ]（k∈Z） | D． | [-$\frac{3}{8}$π+2kπ，$\frac{π}{8}$+2kπ]（k∈Z） |