题目内容
15．在正方形ABCD的边上任取一点M，则点M刚好取自边AB上的概率为$\frac{1}{4}$．分析 利用长度为测度，即可得出结论．
解答 解：设正方形的边长为1，则周长为4，
∴在正方形ABCD的边上任取一点M，点M刚好取自边AB上的概率为$\frac{1}{4}$，
故答案为$\frac{1}{4}$．
点评 本题考查几何概型，确定测度是关键，比较基础．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
6．某企业生产甲、乙两种产品均需用A，B两种原料．已知生产1吨每种产品需原料及每天原料的可用限额如表所示：
（1）设该企业每天生产甲、乙两种产品分别为x，y吨，试写出关于的线性约束条件并画出可行域；
（2）如果生产1吨甲、乙产品可获利润分别为3万元、4万元，试求该企业每天可获得的最大利润．
| 甲 | 乙 | 原料限额 | |
| A（吨） | 3 | 2 | 12 |
| B（吨） | 1 | 2 | 8 |
（2）如果生产1吨甲、乙产品可获利润分别为3万元、4万元，试求该企业每天可获得的最大利润．
3．已知直线l1：3x+4y=0和l2：3x-4y=0的倾斜角（ ）
| A． | 互补 | B． | 互余 | C． | 相等 | D． | 互为相反数 |
10．已知函数$f（x）={cos^2}x+sinx，x∈[\frac{π}{3}，\frac{5π}{6}]$，则f（x）的最大值与最小值的和为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{9}{4}$ | C． | $\frac{{2\sqrt{3}+5}}{4}$ | D． | $\frac{{2\sqrt{3}+6}}{4}$ |
7．某公司生产一种产品，固定成本为20 000元，每生产一单位的产品，成本增加100元，若总收入R与年产量x（0≤x≤390）的关系是$R（x）=-\frac{x^3}{9000}+400x，0≤x≤390$，则当总利润最大时，每年生产的产品单位数是（ ）
| A． | 300 | B． | 250 | C． | 200 | D． | 100 |
4．
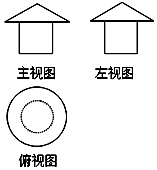如图是一个空间几何体的三视图，其中主视图上半部分是一个底面边长为4、高为1的等腰三角形，主视图下半部分是一个边长为2的正方形，则该空间几何体的体积是（ ）
如图是一个空间几何体的三视图，其中主视图上半部分是一个底面边长为4、高为1的等腰三角形，主视图下半部分是一个边长为2的正方形，则该空间几何体的体积是（ ）| A． | $（8+2\sqrt{5}）π$ | B． | $\frac{10π}{3}$ | C． | $（10+2\sqrt{5}）π$ | D． | $\frac{8π}{3}$ |
5．已知一个几何体的三视图如图所示，则该几何体的体积为（ ）
| A． | $16\sqrt{3}$ | B． | $24\sqrt{3}$ | C． | $\frac{{80\sqrt{3}}}{3}$ | D． | $26\sqrt{3}$ |