某企业生产甲.乙两种产品均需用A.B两种原料．已知生产1吨每种产品需原料及每天原料的可用限额如表所示: 甲乙原料限额 A(吨) 3 2 12 B(吨) 1 2 8(1)设该企业每天生产甲.乙两种产品分别为x.y吨.试写出关于的线性约束条件并画出可行域,(2)如果生产1吨甲.乙产品可获利润分别为3万元.4万元.试求该企业每天可获得的最大利润．题目和参考答案——青夏教育精英家教网—

题目内容

6．某企业生产甲、乙两种产品均需用A，B两种原料．已知生产1吨每种产品需原料及每天原料的可用限额如表所示：

	甲	乙	原料限额
A（吨）	3	2	12
B（吨）	1	2	8

（1）设该企业每天生产甲、乙两种产品分别为x，y吨，试写出关于的线性约束条件并画出可行域；
（2）如果生产1吨甲、乙产品可获利润分别为3万元、4万元，试求该企业每天可获得的最大利润．

分析（1）直接由题意得到关于x，y的线性约束条件并画出可行域；
（2）设该企业每天可获得的利润为z，则z=3x+4y，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数得答案．

解答解：（1）由题意可得：$\left\{\begin{array}{l}{3x+2y≤12}\\{x+2y≤8}\\{x≥0，y≥0}\end{array}\right.$，画出可行域如图：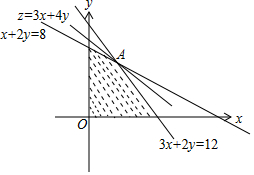

（2）该企业每天可获得的利润为z，则z=3x+4y，
联立$\left\{\begin{array}{l}{3x+2y=12}\\{x+2y=8}\end{array}\right.$，解得A（2，3），
化z=3x+4y为y=-$\frac{3}{4}x+\frac{z}{4}$，
由图可知，当直线y=-$\frac{3}{4}x+\frac{z}{4}$过A时，直线在y轴上的截距最大，z有最大值为3×2+4×3=18．
即该企业每天可获得的最大利润为18万元．

点评本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．

练习册系列答案

17．已知集合A={x|-1≤2x+1≤3}，B={y|y=（x+1）²，x∈A}，则∁_RA∩B=（　　）

14．在△ABC中，a，b，c分别为内角A，B，C的对边，且$cos2C=-\frac{1}{4}$，$0＜C＜\frac{π}{2}$．
（1）求cosC的值；
（2）当a=2，2sinA=sinC时，求b及c的长．

1．设命题p：?n∈N，n²＞2ⁿ，则?p为（　　）

11．脱贫是政府关注民生的重要任务，了解居民的实际收入状况就显得尤为重要．现从某地区随机抽取100个农户，考察每个农户的年收入与年积蓄的情况进行分析，设第i个农户的年收入x_i（万元），年积蓄y_i（万元），经过数据处理得$\sum_{i=1}^{100}{x_i}=500，\sum_{i=1}^{100}{y_i}=100，\sum_{i=1}^{100}{{x_i}{y_i}=1000，}\sum_{i=1}^{100}{x_i^2}=3750$．
（Ⅰ）已知家庭的年结余y对年收入x具有线性相关关系，求线性回归方程；
（Ⅱ）若该地区的农户年积蓄在5万以上，即称该农户已达小康生活，请预测农户达到小康生活的最低年收入应为多少万元？
附：在$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中，$\stackrel{∧}{b}$=$\frac{{{\sum_{i=1}^{n}x}_{i}y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-{n\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$，其中$\overline x，\overline y$为样本平均值．

18．已知f（α）=$\frac{tan（π-α）•cos（2π-α）•sin（\frac{π}{2}+α）}{cos（π+α）}$
（1）化简f（α）
（2）若f（$\frac{π}{2}$-α）=-$\frac{3}{5}$，且α是第二象限角，求tanα

15．在正方形ABCD的边上任取一点M，则点M刚好取自边AB上的概率为$\frac{1}{4}$．

16．执行如图所示的程序框图，正确的是（　　）

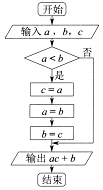
	A．	若输入a，b，c的值依次为1，2，3，则输出的值为5
	B．	若输入a，b，c的值依次为1，2，3，则输出的值为7
	C．	若输入a，b，c的值依次为2，3，4，则输出的值为8
	D．	若输入a，b，c的值依次为2，3，4，则输出的值为10

试题分类