题目内容
10.已知函数$f(x)={cos^2}x+sinx,x∈[\frac{π}{3},\frac{5π}{6}]$,则f(x)的最大值与最小值的和为( )| A. | $\frac{1}{4}$ | B. | $\frac{9}{4}$ | C. | $\frac{{2\sqrt{3}+5}}{4}$ | D. | $\frac{{2\sqrt{3}+6}}{4}$ |
分析 x∈$[\frac{π}{3},\frac{5π}{6}]$,可得sinx∈$[\frac{1}{2},1]$.f(x)=1-sin2x+sinx=-$(sinx-\frac{1}{2})^{2}$+$\frac{5}{4}$,利用二次函数与三角函数的单调性即可得出.
解答 解:∵x∈$[\frac{π}{3},\frac{5π}{6}]$,∴sinx∈$[\frac{1}{2},1]$.
∴f(x)=1-sin2x+sinx=-$(sinx-\frac{1}{2})^{2}$+$\frac{5}{4}$∈$[1,\frac{5}{4}]$.
∴则f(x)的最大值与最小值的和=$\frac{9}{4}$.
故选:B.
点评 本题考查了二次函数与三角函数的单调性与值域,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.设命题p:?n∈N,n2>2n,则?p为( )
| A. | ?n∈N,n2>2n | B. | ?n∈N,n2>2n | C. | ?n∈N,n2≤2n | D. | ?n∈N,n2≤2n |
2.函数f(x)=Asin(ωx+φ)(ω>0,0<φ<π)的一段图象如图所示,则f(x)的解析式为( )
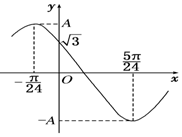

| A. | $y=2sin(4x+\frac{2π}{3})$ | B. | $y=4sin(2x+\frac{π}{3})$ | C. | $y=2\sqrt{3}sin(4x+\frac{π}{6})$ | D. | $y=-2sin(4x+\frac{2π}{3})$ |
20.已知命题p:“1,b,4”成等比数列”,命题q:“b=2”,那么p成立是q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |