题目内容
函数f(x)=Asin(ωx-
)(A>0,ω>0)的最大值为2,相邻两条对称轴的距离为
,则f(x)= .
| π |
| 4 |
| π |
| 2 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:由函数的最大值求出A,由周期求出ω,可得函数的解析式.
解答:
解:由函数的最大值为2,可得A=2,
再根据函数的图象相邻两条对称轴之间的距离为
,可得
•
=
,求得ω=2,
∴函数f(x)=2sin(2x-
),
故答案为:2sin(2x-
).
再根据函数的图象相邻两条对称轴之间的距离为
| π |
| 2 |
| 1 |
| 2 |
| 2π |
| ω |
| π |
| 2 |
∴函数f(x)=2sin(2x-
| π |
| 4 |
故答案为:2sin(2x-
| π |
| 4 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,正弦函数的图象和性质,属于基础题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式x[f(x)-f(-x)]<0的解集为( )
| A、(-1,0)∪(1,+∞) |
| B、(-1,0)∪(0,1) |
| C、(-∞,-1)∪(0,1) |
| D、(-∞,-1)∪(1,+∞) |
设双曲线C1,抛物线C2的焦点均在x轴上,C1的中心与C2的顶点均为原点,从每条曲线上至少取一个点,将其坐标记录如下:
则在C1和C2上点的个数分别是( )
| x | 1 |
|
| 2 | 3 | ||||||
| y | 2
|
| 2 | 4 | 2
|
| A、1,4 | B、2,3 |
| C、4,1 | D、3,3 |
若命题p:2n-1(n∈Z)是奇数;q:2n+1(n∈Z)是偶数,则下列说法中正确的是( )
| A、¬p为真 | B、¬q为假 |
| C、p∨q为真 | D、p∧q为真 |
若实数x,y满足
,若z=x+2y,则z的最大值为( )
|
| A、1 | B、2 | C、3 | D、4 |
阅读右图所示的程序框图,运行相应的程序,输出n的值是( )


| A、2 | B、3 | C、4 | D、5 |
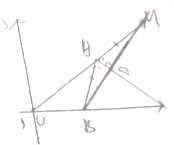 如图,△ABC的周长为8,C(0,0),B(2,0),过B的直线与∠CAB的外角平分线垂直,且交AC的延长线于M,求点M的轨迹方程.
如图,△ABC的周长为8,C(0,0),B(2,0),过B的直线与∠CAB的外角平分线垂直,且交AC的延长线于M,求点M的轨迹方程.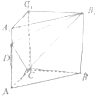 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,四边形BCC1B1是边长为4的正方形,直线AB与平面ACC1A1所成角的正切值为2,点D为棱AA1上的动点.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,四边形BCC1B1是边长为4的正方形,直线AB与平面ACC1A1所成角的正切值为2,点D为棱AA1上的动点.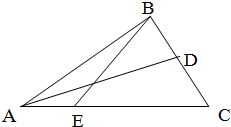 如图,在△ABC中,D是BC的中点,E是AC的三等分点,且EC=2AE,若
如图,在△ABC中,D是BC的中点,E是AC的三等分点,且EC=2AE,若