Question

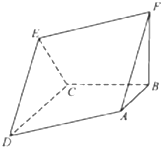如图所示，四边形ADEF为平行四边形，直线FB⊥平面ABCD，AB∥DC，AB⊥BC，AB=BC=FB=1，CD=2．
（Ⅰ）求证：平面CDE⊥平面ABCD；
（Ⅱ）求二面角A-DE-C的余弦值．

Answer 1

考点：二面角的平面角及求法,平面与平面垂直的判定

专题：空间位置关系与距离,空间角

分析：（Ⅰ）取CD中点为G，连结EG，BG，由已知得ABGD为平行四边形，BFEG为平行四边形，从而EG⊥平面ABCD，由此能证明平面CDE⊥平面ABCD．
（Ⅱ）以B为原点，分别以BC，BA，BF为x轴，y轴，z轴，建立空间直角坐标系，利用向量法能求出二面角A-DE-C的余弦值．

解答： （Ⅰ）证明：取CD中点为G，连结EG，BG，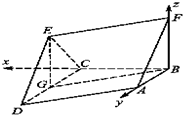
∵AB∥DG，且AB=DG，∴ABGD为平行四边形，
∴BG∥AD，且BG=AD，
又在平行四边形ADEF中，EF∥AD，且EF=AD，
∴BG∥FE，且BG=FE，
∴BFEG为平行四边形，∴BF∥EG，且BF=EG，
∵FB⊥平面ABCD，∴EG⊥平面ABCD，
又EC?平面CDE，∴平面CDE⊥平面ABCD．
（Ⅱ）解：以B为原点，分别以BC，BA，BF为x轴，y轴，z轴，
建立空间直角坐标系，
由已知得A（0，1，0），E（1，1，1），D（1，2，0），C（1，0，0），
则

DA

=（-1，-1，0），

DE

=（0，-1，1），
设

n

=（x，y，z）为平面ADE的一个法向量，
∴

n • DE =-y+z=0 n • DA =-x-y=0

，取y=1，得

n

=（-1，1，1），
由（Ⅰ）得BC⊥平面ECD，∴平面ECD的一个法向量为

BC

=（1，0，0），
∴cos＜

n

，

BC

＞=

n • BC

| n |•| BC |

=-

3

3

，
∵二面角A-DE-C的大小于＜

n

，

BC

＞互补，
∴二面角A-DE-C的余弦值为

3

3

．

点评：本题考查平面与平面垂直的证明，考查二面角的余弦值的求法，解题时要认真审题，注意向量法的合理运用．