题目内容
经过抛物线x2=4y的焦点和双曲线
-
=1的右焦点的直线方程为( )
| x2 |
| 4 |
| y2 |
| 5 |
| A、3x+y-3=0 |
| B、x+3y-3=0 |
| C、x+48y-3=0 |
| D、48x+y-3=0 |
考点:抛物线的标准方程,双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:求出抛物线x2=4y的焦点坐标、双曲线
-
=1的右焦点,即可求出直线方程.
| x2 |
| 4 |
| y2 |
| 5 |
解答:
解:抛物线x2=4y的焦点坐标为(0,1),
双曲线
-
=1的右焦点的坐标为(3,0),
∴所求直线方程为
+y=1,
即x+3y-3=0.
故选:B.
双曲线
| x2 |
| 4 |
| y2 |
| 5 |
∴所求直线方程为
| x |
| 3 |
即x+3y-3=0.
故选:B.
点评:本题考查抛物线、双曲线的性质,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
若函数y=ax-(b+1)(a>0,a≠1)的图象在第一、三、四象限,则有( )
| A、a>1且b<1 |
| B、a>1且b>0 |
| C、0<a<1且b>0 |
| D、0<a<1且b<0 |
计算(log2
+log83)(log32+log92)的结果为 ( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列命题中错误的是( )
A、|x+
| ||||
B、x2+
| ||||
C、
| ||||
D、
|
已知全集U={1,2,3,4,5},集合A={1,2,3},B={3,4,5},图中阴影部分所表示的集合为( )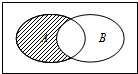

| A、{3} |
| B、{1,2} |
| C、{4,5} |
| D、{1,2,3,4,5} |