题目内容
已知函数f(x)=loga(ax2-x+
)(a>0且a≠1)在[1,2]上恒正,则实数a的取值范围为 .
| 1 |
| 2 |
考点:对数函数图象与性质的综合应用
专题:空间位置关系与距离
分析:分0<a<1和a>1两种情况,结合函数f(x)=loga(ax2-x+
)(a>0且a≠1)在[1,2]上恒正,将问题转化为恒成立问题,求出相应的满足条件的实数a的取值范围,最后综合讨论结果,可得答案.
| 1 |
| 2 |
解答:
解:若0<a<1,
由函数f(x)=loga(ax2-x+
)在[1,2]上恒正可得:
0<ax2-x+
<1在[1,2]上恒成立,
解得:a∈(
,
),
若a>1,
由函数f(x)=loga(ax2-x+
)在[1,2]上恒正可得:
ax2-x+
>1在[1,2]上恒成立,
解得:a∈(
,+∞)
综上所述,实数a的取值范围为:(
,
)∪(
,+∞),
故答案为:(
,
)∪(
,+∞)
由函数f(x)=loga(ax2-x+
| 1 |
| 2 |
0<ax2-x+
| 1 |
| 2 |
解得:a∈(
| 1 |
| 2 |
| 5 |
| 8 |
若a>1,
由函数f(x)=loga(ax2-x+
| 1 |
| 2 |
ax2-x+
| 1 |
| 2 |
解得:a∈(
| 3 |
| 2 |
综上所述,实数a的取值范围为:(
| 1 |
| 2 |
| 5 |
| 8 |
| 3 |
| 2 |
故答案为:(
| 1 |
| 2 |
| 5 |
| 8 |
| 3 |
| 2 |
点评:本题考查的知识点是对数函数图象与性质,恒成立问题,有一定的综合性,考查了转化思想,函数也方程思想和分类讨论思想,难度中档.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
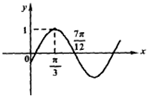 已知导函数f′(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知导函数f′(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
A、先把各点的横坐标缩短到原来的
| ||||
B、先把各点的横坐标伸长到原来的2倍,再向右平移
| ||||
C、先把各点的横坐标缩短到原来的
| ||||
D、先把各点的横坐标伸长到原来的2倍,再向左平移
|