题目内容
设不等式组
所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n)(n∈N*)
(1)求f(1),f(2)的值及f(n)的表达式;
(2)设Sn为数列{bn}的前n项的和,其中bn=2f(n),问是否存在正整数n,t,使
<
成立?若存在,求出正整数n,t;若不存在,说明理由.
|
(1)求f(1),f(2)的值及f(n)的表达式;
(2)设Sn为数列{bn}的前n项的和,其中bn=2f(n),问是否存在正整数n,t,使
| Sn-tbn |
| Sn+1-tbn+1 |
| 1 |
| 16 |
考点:简单线性规划
专题:等差数列与等比数列,不等式的解法及应用
分析:(1)作出不等式组对应的平面区域,根据定义分别求f(1),f(2)的值及f(n)的表达式;
(2)求出Sn,解不等式即可得到结论.
(2)求出Sn,解不等式即可得到结论.
解答:
解:(1)f(1)=3,f(2)=6,
当x=1时,y取值为1,2,3,…,2n,共有2n个格点,
当x=2时,y取值为1,2,3,…,n,共有n个格点,
∴f(n)=n+2n=3n.
(2)bn=2f(n)=23n=8n,为等比数列,
则Sn=
=
(8n-1),
将Sn代入
<
,
化简得
<
,
当t=1,
<
,①,即
<
,此时n=1,
当t>1,有(
-t)8n-
<0,则①式可化为(
-t)8n>
,不可能成立.
综上存在正整数n=1,t=1使
<
成立.
当x=1时,y取值为1,2,3,…,2n,共有2n个格点,
当x=2时,y取值为1,2,3,…,n,共有n个格点,
∴f(n)=n+2n=3n.
(2)bn=2f(n)=23n=8n,为等比数列,
则Sn=
| 8(1-8n) |
| 1-8 |
| 8 |
| 7 |
将Sn代入
| Sn-tbn |
| Sn+1-tbn+1 |
| 1 |
| 16 |
化简得
(
| ||||
(
|
| 1 |
| 2 |
当t=1,
| ||||
|
| 1 |
| 2 |
| 8n |
| 7 |
| 15 |
| 7 |
当t>1,有(
| 8 |
| 7 |
| 1 |
| 7 |
| 8 |
| 7 |
| 15 |
| 7 |
综上存在正整数n=1,t=1使
| Sn-tbn |
| Sn+1-tbn+1 |
| 1 |
| 16 |
点评:本题主要考查线性规划的应用以及等比数列的通项公式和前n项和的计算,考查学生的计算能力.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
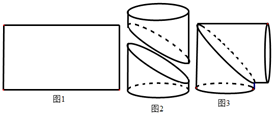 工人师傅在如图1的一块矩形铁皮上画一条曲线,沿曲线剪开,将所得到的两部分卷成圆柱状,如图2,然后将其对接,可做成一个直角的“拐脖”,如图3.工人师傅所画的曲线是( )
工人师傅在如图1的一块矩形铁皮上画一条曲线,沿曲线剪开,将所得到的两部分卷成圆柱状,如图2,然后将其对接,可做成一个直角的“拐脖”,如图3.工人师傅所画的曲线是( )| A、一段圆弧 |
| B、一段抛物线 |
| C、一段双曲线 |
| D、一段正弦曲线 |
在△ABC中,A,B,C所对的边分别是a,b,c,满足3a2+3b2=c2+4ab,现设f(x)=tanx,则( )
| A、f(sinA)≤f(cosB) |
| B、f(sinA)≥f(cosB) |
| C、f(sinA)≤f(sinB) |
| D、f(cosA)≤f(cosB) |
已知A={x|
>1},B={x||x|<a},若∅?B⊆A,则实数a的取值范围是( )
| 4 |
| x+1 |
| A、a<1 | B、a≤1 |
| C、1≤a≤3 | D、0<a≤1 |