题目内容
化简：2sin22α+
sin4α-
•
．
| 3 |
| 4tan2α |
| sin8α |
| 1-tan22α |
| (1+tan22α)2 |
考点：三角函数中的恒等变换应用
专题：三角函数的求值
分析：根据式子的特点利用商的关系切化弦，再通分、利用二倍角的正弦、余弦公式，平方关系，两角和正弦公式进行化简．
解答：
解：原式=2sin22α+
sin4α-
•
=2sin22α+
sin4α-
•
=2sin22α+
sin4α-
•cos4α•cos22α
=2sin22α+
sin4α-
=2sin22α+
sin4α-1
=cos4α+
sin4α
=2sin（4α+
）
| 3 |
4
| ||
| 2sin4αcos4α |
1-
| ||
(1+
|
=2sin22α+
| 3 |
| 2sin2α |
| sin4αcos4αcos2α |
| cos22α-sin22α | ||
|
=2sin22α+
| 3 |
| 2sin2α |
| sin4αcos4αcos2α |
=2sin22α+
| 3 |
| 2sin2α•cos2α |
| sin4α |
=2sin22α+
| 3 |
=cos4α+
| 3 |
=2sin（4α+
| π |
| 6 |
点评：本题考查了二倍角的正弦、余弦公式，以及商的关系，平方关系，两角和正弦公式的灵活应用，基本原则：切化弦，熟练应用三角函数的公式是关键．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
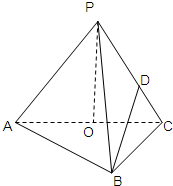如图，在三棱锥P-ABC，AB⊥BC，AB=BC=kPA，点O、D分别是AC、PC的中点，OP⊥底面ABC．