题目内容
设数列的首项a1=a(a≠
),an+1=
(k∈N*),且bn=a2n-1-
(n∈N*).
(1)求a2,a3;
(2)判断数列{bn}是否为等比数列,并证明你的结论;
(3)求
(b1+b2+…+bn).
| 1 |
| 4 |
|
| 1 |
| 4 |
(1)求a2,a3;
(2)判断数列{bn}是否为等比数列,并证明你的结论;
(3)求
| lim |
| n→∞ |
考点:数列的极限,数列递推式
专题:等差数列与等比数列
分析:(1)利用an+1=
(k∈N*),分别取n=1,2即可得出;
(2)由于bn=a2n-1-
(n∈N*),可得bn+1=a2n+1-
=
a2n-
=
(a2n-1+
)-
=
(a2n-1-
)=
bn,即可证明数列{bn}是等比数列.
(3)由(2)可得bn=(a-
)•(
)n-1.再利用等比数列的前n项和公式及其数列极限的运算法则即可得出.
|
(2)由于bn=a2n-1-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
(3)由(2)可得bn=(a-
| 1 |
| 4 |
| 1 |
| 2 |
解答:
解:(1)∵an+1=
(k∈N*),a1=a.
∴a2=a1+
=a+
,a3=
a2=
a+
.
(2)数列{bn}是等比数列,下面给出证明.
∵bn=a2n-1-
(n∈N*),
∴bn+1=a2n+1-
=
a2n-
=
(a2n-1+
)-
=
(a2n-1-
)=
bn,
∴数列{bn}是等比数列,首项b1=a1-
=a-
(a≠
),公比为
.
(3)由(2)可得bn=(a-
)•(
)n-1.
∴b1+b2+…+bn=
=2(a-
)(1-
).
∴
(b1+b2+…+bn)=
2(a-
)(1-
)=2a-
.
|
∴a2=a1+
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
(2)数列{bn}是等比数列,下面给出证明.
∵bn=a2n-1-
| 1 |
| 4 |
∴bn+1=a2n+1-
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
∴数列{bn}是等比数列,首项b1=a1-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
(3)由(2)可得bn=(a-
| 1 |
| 4 |
| 1 |
| 2 |
∴b1+b2+…+bn=
(a-
| ||||
1-
|
| 1 |
| 4 |
| 1 |
| 2n |
∴
| lim |
| n→∞ |
| lim |
| n→∞ |
| 1 |
| 4 |
| 1 |
| 2n |
| 1 |
| 2 |
点评:本题考查了分段数列的意义、等比数列的通项公式及其前n项和公式、数列极限的运算法则,考查了推理能力与计算能力,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知P是圆O外一点,PE切圆O于点E,B、F是圆O上一点,PB交圆O于A点,EF∥AP,BE:BF=3:4,PE=4,则AB=
已知P是圆O外一点,PE切圆O于点E,B、F是圆O上一点,PB交圆O于A点,EF∥AP,BE:BF=3:4,PE=4,则AB=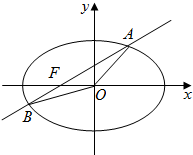 已知椭圆
已知椭圆