题目内容
直线y=-
x+
与圆x2+y2=4相交于A、B两点,则弦AB的长度为( )
| 3 |
| 4 |
| 5 |
| 4 |
A、3
| ||
B、2
| ||
C、
| ||
| D、1 |
考点:直线与圆相交的性质
专题:直线与圆
分析:先求出圆心(0,0)到直线y=-
x+
的距离为d的值,再根据半径为2,利用弦长公式求得弦AB的长度.
| 3 |
| 4 |
| 5 |
| 4 |
解答:
解:圆心(0,0)到直线y=-
x+
的距离为d=
=1,而圆的半径为2,故弦长为2
=2
,
故选:B.
| 3 |
| 4 |
| 5 |
| 4 |
|0+0-
| ||||
|
| r2-d2 |
| 3 |
故选:B.
点评:本题主要考查直线和圆相交的性质,点到直线的距离公式,弦长公式的应用,属于基础题.

练习册系列答案
相关题目
到两定点F1(-3,0)、F2(3,0)的距离之差的绝对值等于6的点M的轨迹( )
| A、两条射线 | B、线段 |
| C、双曲线 | D、椭圆 |
钝角△ABC最大边长为4,其余两边长为x,y,以(x,y)为坐标的点所表示的平面区域的面积为( )
| A、4π-8 | ||
| B、4π+8 | ||
| C、4π-6 | ||
D、4π-
|
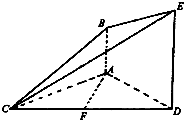 如图,已知DE⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB=2,且F是CD的中点.
如图,已知DE⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB=2,且F是CD的中点.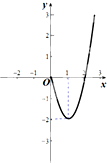 已知定义在R上奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分.
已知定义在R上奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分.