题目内容
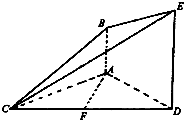 如图,已知DE⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB=2,且F是CD的中点.
如图,已知DE⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB=2,且F是CD的中点.(1)求证:AF∥平面BCE;
(2)求四棱锥C-ABED的全面积.
考点:棱柱、棱锥、棱台的侧面积和表面积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)取CE中点P,连结FP,BP,证明ABPF为平行四边形,然后利用直线余平面平行的判定定理证明AF∥平面BCE.
(2)求出SABED,S△ACD=
,S△CDE,S△ABC,S△BCW,然后求出全面积.
(2)求出SABED,S△ACD=
| 3 |
解答:
解:(1)证明:取CE中点P,连结FP,BP
∵F为CD的中点,∴FP
DE
又AB
DE∴AB
FP
∴ABPF为平行四边形,∴AF∥BP
又∵AF?平面BCE,BP?平面BCE,∴AF∥平面BCE.
(2)SABED=
×2=3,S△ACD=
×
×2=
,
S△CDE=
×2×2=2,S△ABC=
×2×1=1,S△BCE=
CE•AF=
×2
×
=
S全=6+
+
.

∵F为CD的中点,∴FP
| ||
. |
| 1 |
| 2 |
又AB
| ||
. |
| 1 |
| 2 |
| ||
. |
∴ABPF为平行四边形,∴AF∥BP
又∵AF?平面BCE,BP?平面BCE,∴AF∥平面BCE.
(2)SABED=
| 1+2 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
S△CDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 6 |
S全=6+
| 3 |
| 6 |
点评:本题考查直线与平面平行的判定定理的应用,几何体的表面积的求法,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
命题“任意x∈R,x2+2x+2>0”的否定是( )
| A、任意x∈R,x2+2x+2≤0 |
| B、不存在x∈R,x2+2x+2>0 |
| C、存在x∈R,x2+2x+2≤0 |
| D、存在x∈R,x2+2x+2>0 |
等差数列{an}的前n项和为Sn,S3=6,a2+a4=0,公差d为( )
| A、1 | B、-3 | C、-2 | D、3 |
已知集合M={x|-4≤x≤7},N={x|x2-x-12>0},则M∩N为( )
| A、{x|-4≤x<-3或4<x≤7} |
| B、{x|-4<x≤-3或4≤x<7} |
| C、{x|x≤-3或x>4} |
| D、{x|x<-3或x≥4} |
直线y=-
x+
与圆x2+y2=4相交于A、B两点,则弦AB的长度为( )
| 3 |
| 4 |
| 5 |
| 4 |
A、3
| ||
B、2
| ||
C、
| ||
| D、1 |