题目内容
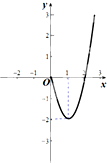 已知定义在R上奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分.
已知定义在R上奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分.(1)请补全函数f(x)的图象;
(2)写出函数f(x)的表达式(只写明结果,无需过程);
(3)讨论方程|f(x)|=a的解的个数(只写明结果,无需过程).
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:(1)补全f(x)的图象如图1所示:
(2)当x≥0时,设f(x)=a(x-1)2-2,由f(0)=0求得a的值,可得函数的解析式;再利用函数的奇偶性求得x<0时函数的解析式,综合可得结论.
(3)函数y=|f(x)的图象如图2所示,方程|f(x)|=a的解的个数,即函数f(x)的图象和直线y=a的交点个数,数形结合、分类讨论可得结论.
(2)当x≥0时,设f(x)=a(x-1)2-2,由f(0)=0求得a的值,可得函数的解析式;再利用函数的奇偶性求得x<0时函数的解析式,综合可得结论.
(3)函数y=|f(x)的图象如图2所示,方程|f(x)|=a的解的个数,即函数f(x)的图象和直线y=a的交点个数,数形结合、分类讨论可得结论.
解答:

 解:(1)补全f(x)的图象如图1所示:
解:(1)补全f(x)的图象如图1所示:
(2)当x≥0时,设f(x)=a(x-1)2-2,由f(0)=0得,a=2,
所以此时,f(x)=2(x-1)2-2=2x2-4x.
当x<0时,-x>0,所以 f(-x)=2(-x)2-4(-x)=2x2+4x …①
又f(-x)=-f(x),代入①得 f(x)=-2x2-4x.
综上可得,f(x)=
.
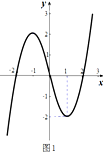
(3)方程|f(x)|=a的解的个数,即函数f(x)的图象和直线y=a的交点个数,函数y=|f(x)的图象如图2所示,
由图象可得,当a<0时,方程无解;当a=0时,方程有三个解;
当0<a<2时,方程有6个解; 当a=2时,方程有4个解;当a>2时,方程有2个解.

 解:(1)补全f(x)的图象如图1所示:
解:(1)补全f(x)的图象如图1所示:(2)当x≥0时,设f(x)=a(x-1)2-2,由f(0)=0得,a=2,
所以此时,f(x)=2(x-1)2-2=2x2-4x.
当x<0时,-x>0,所以 f(-x)=2(-x)2-4(-x)=2x2+4x …①
又f(-x)=-f(x),代入①得 f(x)=-2x2-4x.
综上可得,f(x)=
|
(3)方程|f(x)|=a的解的个数,即函数f(x)的图象和直线y=a的交点个数,函数y=|f(x)的图象如图2所示,
由图象可得,当a<0时,方程无解;当a=0时,方程有三个解;
当0<a<2时,方程有6个解; 当a=2时,方程有4个解;当a>2时,方程有2个解.
点评:本题主要考查根的存在性以及根的个数判断,函数的图象和性质的应用,利用奇函数的性质求函数的解析式,体现了数形结合、分类讨论、等价转化的数学思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合M={x|-4≤x≤7},N={x|x2-x-12>0},则M∩N为( )
| A、{x|-4≤x<-3或4<x≤7} |
| B、{x|-4<x≤-3或4≤x<7} |
| C、{x|x≤-3或x>4} |
| D、{x|x<-3或x≥4} |
如图是一个空间几何体的三视图,则这个几何体的侧面积是( )
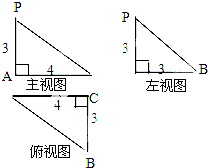

| A、42 | B、21 | C、24 | D、6 |
直线y=-
x+
与圆x2+y2=4相交于A、B两点,则弦AB的长度为( )
| 3 |
| 4 |
| 5 |
| 4 |
A、3
| ||
B、2
| ||
C、
| ||
| D、1 |
数列{an}满足an+1-an+an-1=0(n≥2),且a1=1,a2=-1,则a2013的值为( )
| A、1 | B、-1 | C、2 | D、-2 |