题目内容
钝角△ABC最大边长为4,其余两边长为x,y,以(x,y)为坐标的点所表示的平面区域的面积为( )
| A、4π-8 | ||
| B、4π+8 | ||
| C、4π-6 | ||
D、4π-
|
考点:二元一次不等式(组)与平面区域
专题:不等式的解法及应用
分析:由钝角三角形的性质可得x和y的不等式组,作图可得面积.
解答:
解:∵钝角△ABC最大边长为4,其余两边长为x,y,
∴x,y满足
,作出不等式组对应的平面区域(如图阴影弓形),
可得面积S=
×π×42-
×4×4=4π-8
故选:A

∴x,y满足
|
可得面积S=
| 1 |
| 4 |
| 1 |
| 2 |
故选:A

点评:本题考查不等式组与平面区域,涉及圆的面积公式,属基础题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
如图是一个空间几何体的三视图,则这个几何体的侧面积是( )
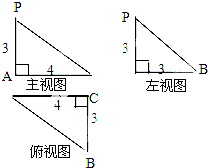

| A、42 | B、21 | C、24 | D、6 |
直线y=-
x+
与圆x2+y2=4相交于A、B两点,则弦AB的长度为( )
| 3 |
| 4 |
| 5 |
| 4 |
A、3
| ||
B、2
| ||
C、
| ||
| D、1 |
直线y=kx-2与椭圆x2+4y2=80相交于不同的两点P、Q,若PQ的中点横坐标为2,则直线的斜率等于( )
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |