题目内容
在△ABC中,cosA:cosB:sinC=a:b:c,则△ABC的形状为 .
考点:正弦定理
专题:解三角形
分析:由已知,结合正弦定理容易得到sinA=cosA,sinB=cosB,从而得到A=B=45°.
解答:
解:由正弦定理,sinA:sinB:sinC=a:b:c,结合cosA:cosB:sinC=a:b:c,即sinA=cosA,sinB=cosB,得A=B=
.
故△ABC的形状为:等腰直角三角形.
故答案为:等腰直角三角形.
| π |
| 4 |
故△ABC的形状为:等腰直角三角形.
故答案为:等腰直角三角形.
点评:本题考查了正弦定理的运用,关键是利用正弦定理得到sinA=cosA,sinB=cosB,求出A,B,判断三角形的形状.

练习册系列答案
相关题目
等差数列{an}的前n项和为Sn,S3=6,a2+a4=0,公差d为( )
| A、1 | B、-3 | C、-2 | D、3 |
如图是一个空间几何体的三视图,则这个几何体的侧面积是( )
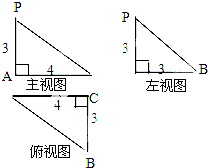

| A、42 | B、21 | C、24 | D、6 |
直线y=-
x+
与圆x2+y2=4相交于A、B两点,则弦AB的长度为( )
| 3 |
| 4 |
| 5 |
| 4 |
A、3
| ||
B、2
| ||
C、
| ||
| D、1 |