题目内容
4．正六棱柱ABCDEF-A1B1C1D1E1F1的底面边长为$\sqrt{3}$，侧棱长为1，则动点从A沿表面移动到点D1时的最短的路程是$\sqrt{19}$．分析 根据题意，画出图形，结合图形得出从A点沿表面到D1的路程是多少，求出即可．
解答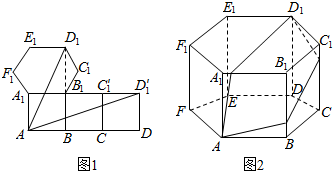 
解：将所给的正六棱柱按图1部分展开，
则AD′1=$\sqrt{{4}^{2}{+（\sqrt{3}）}^{2}}$=$\sqrt{19}$，
AD1=$\sqrt{{1}^{2}{+（3\sqrt{3}）}^{2}}$=$\sqrt{28}$，
∵AD′1＜AD1，
∴从A点沿正侧面和上底面到D1的路程最短，为$\sqrt{19}$．
故答案为：$\sqrt{19}$．
点评 本题考查了几何体的展开图，以及两点之间线段最短的应用问题，立体几何两点间的最短距离时，通常把立体图形展开成平面图形，转化成平面图形两点间的距离问题来求解，是基础题目．
练习册系列答案
相关题目
12．已知点P在以F1，F2为焦点的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上，若$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0，tan∠PF1F2=$\frac{1}{2}$，则该椭圆的离心率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{\sqrt{5}}{3}$ |