题目内容
已知向量
,
满足|
|=1,|
|=4,且
•
≥2,则
与
的夹角的取值范围是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、[
| ||
B、(0,
| ||
C、[0,
| ||
D、[
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由向量数量积的定义:
•
=|
|•|
|cosθ=1×4cosθ≥2,再由向量夹角的取值范围求解.
| a |
| b |
| a |
| b |
解答:
解:设
与
的夹角θ,∵
•
=|
|•|
|cosθ=1×4cosθ≥2,
∴cosθ≥
,
∵θ∈[0,π]
∴θ∈[0,
].
故选C.
| a |
| b |
| a |
| b |
| a |
| b |
∴cosθ≥
| 1 |
| 2 |
∵θ∈[0,π]
∴θ∈[0,
| π |
| 3 |
故选C.
点评:本题考察了向量数量积的运算,运用求夹角问题,难度不大.

练习册系列答案
相关题目
将曲线y2=4x按ϕ:
变换后得到曲线的焦点坐标为( )
|
A、(
| ||
B、(
| ||
C、.(
| ||
| D、(1,0) |
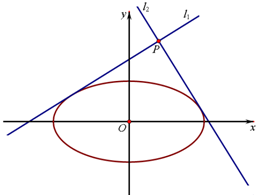 已知椭圆C:
已知椭圆C: