题目内容
设M={0，1，2，4，5，7}，N={1，4，6，8，9}，P={4，7，9}，则（M∩N）∪（M∩P）= ．
考点：交、并、补集的混合运算
专题：集合
分析：根据题意和交集的运算求出M∩N、M∩P，再由并集的运算求出（M∩N）∪（M∩P）．
解答：
解：由M={0，1，2，4，5，7}、N={1，4，6，8，9}得，M∩N={1，4}，
又P={4，7，9}，则M∩P={4，7}，
所以（M∩N）∪（M∩P）={1，4，7}，
故答案为：{1，4，7}．
又P={4，7，9}，则M∩P={4，7}，
所以（M∩N）∪（M∩P）={1，4，7}，
故答案为：{1，4，7}．
点评：本题考查了交、并、补集的混合运算，熟练掌握交、并、补集的运算是解题的关键，属于基础题．
练习册系列答案
相关题目
已知向量
，
满足|
|=1，|
|=4，且
•
≥2，则
与
的夹角的取值范围是（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、[
| ||
B、（0，
| ||
C、[0，
| ||
D、[
|
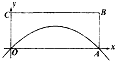为了测量抛物线y=x-x2与x轴所围成的封闭圆形面积，现截取矩形OABC，其中|OA|=1，|AB|=0.4，在该矩形内随机地撒600颗豆，数得落在该封闭圆形部分的豆数为250颗，据此可以估计封闭图形的面积为y=sin（x-
）•cos（x-
），正确的是（ ）
| π |
| 12 |
| π |
| 12 |
A、T=2π，对称中心为（
| ||
B、T=π，对称中心为（
| ||
C、T=2π，对称中心为（
| ||
D、T=π，对称中心为（
|