题目内容
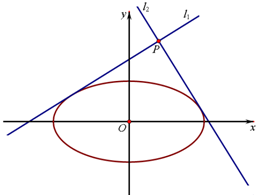 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 4 |
(1)求椭圆C的方程;
(2)求点P的轨迹方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知得2b=6,
=e2=
=
.由此能求出椭圆C的方程.
(2)若直线l1的斜率存在且不为零时,设为k,设P(x0,y0),则直线l1的方程为y=kx+y0-kx0,令m=y0-kx0.
⇒(16k2+9)x2+32kmx+16m2-144=0.由此利用根的判别式、点到直线的距离公式、韦达定理能求出|OP|2=25.直线l1的斜率不存在或为零时也成立,由此能求出点P的轨迹是圆x2+y2=25.
| 7 |
| 16 |
| c2 |
| a2 |
| a2-b2 |
| a2 |
(2)若直线l1的斜率存在且不为零时,设为k,设P(x0,y0),则直线l1的方程为y=kx+y0-kx0,令m=y0-kx0.
|
解答:
解:(1)∵椭圆C:
+
=1(a>b>0)的短轴长为6.其离心率为
.
∴2b=6,解得b=3,又e=
,
从而
=e2=
=
.
解得a2=16,b2=9.
∴椭圆C的方程为
+
=1.…(6分)
(2)①若直线l1的斜率存在且不为零时,设为k,
设P(x0,y0),则直线l1的方程为y-y0=k(x-x0).
即y=kx+y0-kx0,令m=y0-kx0.
⇒(16k2+9)x2+32kmx+16m2-144=0.
直线l1是椭圆的切线,
∴△=(32km)2-4(16k2+9)(16m2-144)=0,∴m2=16k2+9,
坐标原点O到直线l1的距离d1=
,
∴
=
=
.
设坐标原点O到直线l2的距离为d2,
同理可得
=
=
.
所以|OP|2=
+
=
+
=25.
②若直线l1的斜率不存在或为零时,由题意得|OP|2=
+
=25.
综上,|OP|2=25.
∴点P的轨迹是圆x2+y2=25.…(13分)
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 4 |
∴2b=6,解得b=3,又e=
| ||
| 4 |
从而
| 7 |
| 16 |
| c2 |
| a2 |
| a2-b2 |
| a2 |
解得a2=16,b2=9.
∴椭圆C的方程为
| x2 |
| 16 |
| y2 |
| 9 |
(2)①若直线l1的斜率存在且不为零时,设为k,
设P(x0,y0),则直线l1的方程为y-y0=k(x-x0).
即y=kx+y0-kx0,令m=y0-kx0.
|
直线l1是椭圆的切线,
∴△=(32km)2-4(16k2+9)(16m2-144)=0,∴m2=16k2+9,
坐标原点O到直线l1的距离d1=
| |m| | ||
|
∴
| d | 2 1 |
| m2 |
| 1+k2 |
| 16k2+9 |
| 1+k2 |
设坐标原点O到直线l2的距离为d2,
同理可得
| d | 2 2 |
16(-
| ||
1+(-
|
| 9k2+16 |
| 1+k2 |
所以|OP|2=
| d | 2 1 |
| d | 2 2 |
| 16k2+9 |
| 1+k2 |
| 9k2+16 |
| 1+k2 |
②若直线l1的斜率不存在或为零时,由题意得|OP|2=
| d | 2 1 |
| d | 2 2 |
综上,|OP|2=25.
∴点P的轨迹是圆x2+y2=25.…(13分)
点评:本题考查椭圆方程的求法,考查点的轨迹方程的求法,解题时要认真审题,注意根的判别式、点到直线的距离公式、韦达定理的合理运用.

练习册系列答案
相关题目
已知向量
,
满足|
|=1,|
|=4,且
•
≥2,则
与
的夹角的取值范围是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、[
| ||
B、(0,
| ||
C、[0,
| ||
D、[
|
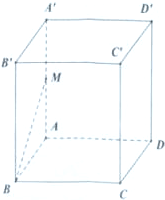 如图,在直平行六面体ABCD-A′B′C′D′中,底面ABCD是边长为2的菱形,∠ABC=60°,A′C与底面ABCD所成角的大小为arctan2,M为A′A的中点.
如图,在直平行六面体ABCD-A′B′C′D′中,底面ABCD是边长为2的菱形,∠ABC=60°,A′C与底面ABCD所成角的大小为arctan2,M为A′A的中点.