题目内容
已知集合M={12，a}，P={x|-1≤x＜2，x∈Z}，M∩P={0}，若M∪P=S，则集合S的真子集个数是 ．
考点：子集与真子集
专题：集合
分析：根据M与P的交集，确定出a的值，确定出M，求出M与P的并集，即为S，找出S的真子集个数即可．
解答：
解：∵M={12，a}，P={x|-1≤x＜2，x∈Z}={-1，0，1}，M∩P={0}，
∴a=0，即M={0，12}，
∴S=M∪P={-1，0，1，12}，
则集合S的真子集个数为24-1=15．
故答案为：15
∴a=0，即M={0，12}，
∴S=M∪P={-1，0，1，12}，
则集合S的真子集个数为24-1=15．
故答案为：15
点评：此题考查了子集与真子集，熟练掌握各自的定义是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
已知向量
，
满足|
|=1，|
|=4，且
•
≥2，则
与
的夹角的取值范围是（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、[
| ||
B、（0，
| ||
C、[0，
| ||
D、[
|
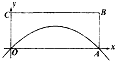为了测量抛物线y=x-x2与x轴所围成的封闭圆形面积，现截取矩形OABC，其中|OA|=1，|AB|=0.4，在该矩形内随机地撒600颗豆，数得落在该封闭圆形部分的豆数为250颗，据此可以估计封闭图形的面积为