题目内容

将曲线y2=4x按ϕ：
x′=2x
2y′=y
变换后得到曲线的焦点坐标为（　　）
A、(
1
8
，0)
B、(
1
4
，0)
C、.(
1
2
，0)
D、（1，0）
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：先根据所给变换得出变换后的抛物线的标准方程，再由所得抛物线的标准方程确定其焦点坐标．
解答： 解：由已知得
x=
1
2
x′
y=2y′
，代入抛物线方程y2=4x得y′2=
1
2
x′，所以其焦点坐标为（
1
8
，0），
故选A．
点评：本题考查变换知识，考查抛物线的方程与性质，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
已知全集 U=R，集合A={x|2≤x≤8}，B={x|1＜x＜6}．
（1）求A∪B，
（2）（∁UA）∩B．
已知向量
a
，
b
满足|
a
|=1，|
b
|=4，且
a
•
b
≥2，则
a
与
b
的夹角的取值范围是（　　）
A、[
π
6
，π]
B、（0，
π
3
]
C、[0，
π
3
]
D、[
π
3
，π]
已知x、y、z是互不相等的正实数，且x+y+z=1．求证：（
1
x
-1）（
1
y
-1）（
1
z
-1）＞8．
将（
3
2
）-0.2，1.10.7，(
2
3
)
1
3
由大到小排列为
 
．
若θ∈（
π
2
，π），则
1-sin2θ
=（　　）
A、cosθ-sinθ
B、sinθ-cosθ
C、cosθ+sinθ
D、-cosθ-sinθ
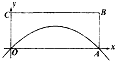为了测量抛物线y=x-x2与x轴所围成的封闭圆形面积，现截取矩形OABC，其中|OA|=1，|AB|=0.4，在该矩形内随机地撒600颗豆，数得落在该封闭圆形部分的豆数为250颗，据此可以估计封闭图形的面积为
 
．
已知数列{an}，{bn}满足：bn=an+1-λan（n∈N*）．
（1）若λ=1，a1=1，bn=2n，求数列{an}的通项公式；
（2）若λ=-1，a1=a，a2=3a，bn=4n-1，且{an}是递增数列，求a的取值范围；
（3）若λ=1，bn+1bn-1=bn（n≥2），且b1=1，b2=2，记cn=a6n-1（n∈N*），求证：数列{cn}为等差数列．
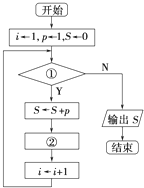给出30个数：1，2，4，7，11，…，其规律是：第1个数是1，第2个数比第1个数大1，第3个数比第2个数大2，第4个数比第3个数大3，依此类推．要计算这30个数的和，现已给出了该问题算法的流程图如图所示．请根据流程图，将下列伪代码补充完整．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网