题目内容
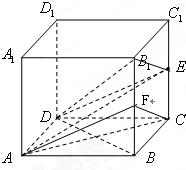 正方体ABCD-A1B1C1D1,AA1=2,E,F分别为棱CC1,BB1的中点.
正方体ABCD-A1B1C1D1,AA1=2,E,F分别为棱CC1,BB1的中点.(1)求三棱锥E-ABC的体积.
(2)求证:平面AFC∥平面B1DE.
考点:平面与平面平行的判定,棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(1)利用三棱锥E-ABC的体积公式,即可得出结论;
(2)由E、F是CC1、BB1的中点,易得AF∥ED,CF∥B1E,从而平面ACF∥面B1DE.
(2)由E、F是CC1、BB1的中点,易得AF∥ED,CF∥B1E,从而平面ACF∥面B1DE.
解答:
解:(1)正方体ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点,
∴三棱锥E-ABC的体积为V=
×
×2×2×1=
;
(2)证明:∵E、F是CC1、BB1的中点,∴CE平行且等于B1F
∴四边形B1FCE是平行四边形,
∴CF∥B1E.
∵E,F是CC1、BB1的中点,∴EF平行且等于BC,
又BC平行且等于AD,∴EF平行且等于AD.
∴四边形ADEF是平行四边形,∴AF∥ED,
∵AF∩CF=F,B1E∩ED=E,
∴平面ACF∥面B1DE.
∴三棱锥E-ABC的体积为V=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
(2)证明:∵E、F是CC1、BB1的中点,∴CE平行且等于B1F
∴四边形B1FCE是平行四边形,
∴CF∥B1E.
∵E,F是CC1、BB1的中点,∴EF平行且等于BC,
又BC平行且等于AD,∴EF平行且等于AD.
∴四边形ADEF是平行四边形,∴AF∥ED,
∵AF∩CF=F,B1E∩ED=E,
∴平面ACF∥面B1DE.
点评:本题主要考查三棱锥E-ABC的体积和面面平行的判定定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
设全集为R,集合A={x|x2-9<0},B={x|-1<x≤5},则A∩B=( )
| A、(3,5] |
| B、(-1,3) |
| C、(-3,-1) |
| D、(-3,5] |
设x,y满足不等式组
则目标函数z=2x+y的最小值是( )
|
A、
| ||
| B、4 | ||
C、
| ||
D、
|
在三棱锥P-ABC中,O是底面正三角形ABC的中心,Q为棱PA上的一点,PA=1,若QO∥平面PBC,则PQ=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知{an}是等差数列,a1+a7=-2,a3=2,则{an}的公差d=( )
| A、-1 | B、-2 | C、-3 | D、-4 |