题目内容
在三棱锥P-ABC中,O是底面正三角形ABC的中心,Q为棱PA上的一点,PA=1,若QO∥平面PBC,则PQ=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:点、线、面间的距离计算
专题:计算题,空间位置关系与距离
分析:设过OQ,且平行于平面PBC的平面与AC,相交于D,则OD∥BC,DQ∥PC,利用三角形的重心的性质,即可得出结论.
解答:
 解:设过OQ,且平行于平面PBC的平面与AC相交于D,则OD∥BC,DQ∥PC,
解:设过OQ,且平行于平面PBC的平面与AC相交于D,则OD∥BC,DQ∥PC,
∵O是底面正三角形ABC的中心,
∴CD=
AC
∴PQ=
PA=
,
故选:C.
 解:设过OQ,且平行于平面PBC的平面与AC相交于D,则OD∥BC,DQ∥PC,
解:设过OQ,且平行于平面PBC的平面与AC相交于D,则OD∥BC,DQ∥PC,∵O是底面正三角形ABC的中心,
∴CD=
| 1 |
| 3 |
∴PQ=
| 1 |
| 3 |
| 1 |
| 3 |
故选:C.
点评:本题考查线面平行,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
函数y=
(0<a<1)的图象的大致形状是( )
| xax |
| |x| |
A、 |
B、 |
C、 |
D、 |
已知双曲线mx2-ny2=1(mn>0)的渐近线方程为y=±
x,此双曲线的离心率为( )
| 3 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
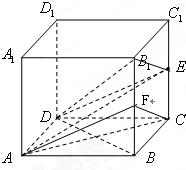 正方体ABCD-A1B1C1D1,AA1=2,E,F分别为棱CC1,BB1的中点.
正方体ABCD-A1B1C1D1,AA1=2,E,F分别为棱CC1,BB1的中点.