题目内容
已知{an}是等差数列,a1+a7=-2,a3=2,则{an}的公差d=( )
| A、-1 | B、-2 | C、-3 | D、-4 |
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:由等差数列的性质结合已知求得a4,再由等差数列的通项公式求得公差.
解答:
解:在等差数列{an}中,由a1+a7=-2,得2a4=-2,即a4=-1,
又a3=2,
∴d=
=
=-3.
故选:C.
又a3=2,
∴d=
| a4-a3 |
| 4-3 |
| -1-2 |
| 4-3 |
故选:C.
点评:本题考查了等差数列的通项公式,考查了等差数列的性质,是基础题.

练习册系列答案
相关题目
椭圆2x2+3y2=6的焦距是( )
| A、2 | ||||
B、2(
| ||||
C、2
| ||||
D、2(
|
已知函数f(x)=sin(x-φ),且
f(x)dx=0,则函数f(x)的图象的一条对称轴是( )
| ∫ |
0 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
已知双曲线mx2-ny2=1(mn>0)的渐近线方程为y=±
x,此双曲线的离心率为( )
| 3 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
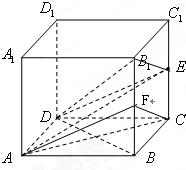 正方体ABCD-A1B1C1D1,AA1=2,E,F分别为棱CC1,BB1的中点.
正方体ABCD-A1B1C1D1,AA1=2,E,F分别为棱CC1,BB1的中点.