题目内容
设x,y满足不等式组
则目标函数z=2x+y的最小值是( )
|
A、
| ||
| B、4 | ||
C、
| ||
D、
|
考点:简单线性规划
专题:数形结合
分析:本题考查的知识点是线性规划,处理的思路为:根据已知的约束条件,画出满足约束条件的可行域,再用角点法,求出目标函数的最大值.
解答:
解:画出满足条件
的平面区域,
如图示:
 ,
,
而z=2x+y可化为:y=-2x+z,
显然y=-2x+z过(0,
)时,z最小为
,
故选:C.
|
如图示:
 ,
,而z=2x+y可化为:y=-2x+z,
显然y=-2x+z过(0,
| 4 |
| 3 |
| 4 |
| 3 |
故选:C.
点评:用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,可先将题目中的量分类、列出表格,理清头绪,然后列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数.然后将可行域各角点的值一一代入,最后比较,即可得到目标函数的最优解.

练习册系列答案
相关题目
函数y=
(0<a<1)的图象的大致形状是( )
| xax |
| |x| |
A、 |
B、 |
C、 |
D、 |
已知函数f(x)=sin(x-φ),且
f(x)dx=0,则函数f(x)的图象的一条对称轴是( )
| ∫ |
0 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
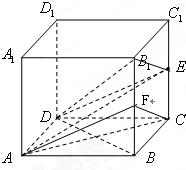 正方体ABCD-A1B1C1D1,AA1=2,E,F分别为棱CC1,BB1的中点.
正方体ABCD-A1B1C1D1,AA1=2,E,F分别为棱CC1,BB1的中点.