题目内容
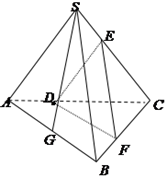如图，在三棱锥S-ABC中，D、E、F分别是棱AC、BC、SC上的点，且CD=2DA，CE=2ES，CF=2FB，G是AB的中点．求证：SG∥平面DEF．考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：利用三角形中位线的性质，证明DE∥AB，利用线面平行的判定定理证明AB∥平面DEF，同理SA∥平面DEF，利用面面平行的判定定理，证明SG∥平面DEF；
解答：
证明：∵D、E分别是AC、BC的中点，
∴DE∥AB，
∵AB?平面DEF，DE?平面DEF，
∴AB∥平面DEF，
同理SA∥平面DEF，
∵AB∩SA=A，
∴平面SAB∥平面DEF，
∵SG?平面SAB，
∴SG∥平面DEF．
∴DE∥AB，
∵AB?平面DEF，DE?平面DEF，
∴AB∥平面DEF，
同理SA∥平面DEF，
∵AB∩SA=A，
∴平面SAB∥平面DEF，
∵SG?平面SAB，
∴SG∥平面DEF．
点评：本题考查线面平行，考查面面平行，正确运用线面平行，面面平行的判定定理是关键，属于基础题．
练习册系列答案
相关题目
正三棱锥S-ABC中，SA=5，AB=4
，则三棱锥S-ABC的体积为（ ）
| 3 |
A、4
| ||
B、8
| ||
C、12
| ||
D、36
|
若θ为三角形的一个内角，且sinθ+cosθ=
，则曲线 x2sinθ+y2cosθ=1是（ ）
| 1 |
| 5 |
| A、焦点在x轴上的双曲线 |
| B、焦点在y轴上的双曲线 |
| C、焦点在x轴上的椭圆 |
| D、焦点在y轴上的椭圆 |
已知
，且z=2x+y的最大值是最小值的3倍，则a的值是（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|