题目内容
已知直二面角α-PQ-β,A∈PQ,B∈α,C∈β,CA=CB,∠BAP=45°,直线CA和平面α所成角为30°,那么二面角B-AC-P的正切值为( )
| A、2 | ||
| B、3 | ||
C、
| ||
D、
|
考点:二面角的平面角及求法
专题:综合题,空间角
分析:在平面β内过点C作CO⊥PQ于点O,连接OB,证明BO⊥PQ.过点O作OH⊥AC于点H,连接BH,由三垂线定理知,BH⊥AC,故∠BHO是二面角B-AC-P的平面角,然后在Rt△BOH中解出此角即可.
解答:
解:在平面β内过点C作CO⊥PQ于点O,连接OB.
因为α⊥β,α∩β=PQ,所以CO⊥α,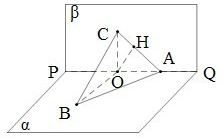
又因为CA=CB,所以OA=OB.
而∠BAO=45°,所以∠ABO=45°,∠AOB=90°.从而BO⊥PQ.
又α⊥β,α∩β=PQ,BO?α,所以BO⊥β.
过点O作OH⊥AC于点H,连接BH,由三垂线定理知,BH⊥AC.
故∠BHO是二面角B-AC-P的平面角.
因为CO⊥α,所以∠CAO是CA和平面α所成的角,则∠CAO=30°,
不妨设AC=2,则AO=
,OH=AOsin30°=
.
在Rt△OAB中,∠ABO=∠BAO=45°,所以BO=AO=
,
于是在Rt△BOH中,tan∠BHO=2.
故选:A.
因为α⊥β,α∩β=PQ,所以CO⊥α,

又因为CA=CB,所以OA=OB.
而∠BAO=45°,所以∠ABO=45°,∠AOB=90°.从而BO⊥PQ.
又α⊥β,α∩β=PQ,BO?α,所以BO⊥β.
过点O作OH⊥AC于点H,连接BH,由三垂线定理知,BH⊥AC.
故∠BHO是二面角B-AC-P的平面角.
因为CO⊥α,所以∠CAO是CA和平面α所成的角,则∠CAO=30°,
不妨设AC=2,则AO=
| 3 |
| ||
| 2 |
在Rt△OAB中,∠ABO=∠BAO=45°,所以BO=AO=
| 3 |
于是在Rt△BOH中,tan∠BHO=2.
故选:A.
点评:本题主要考查了平面与平面之间的位置关系,以及空间中直线与直线之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
正三棱锥S-ABC中,SA=5,AB=4
,则三棱锥S-ABC的体积为( )
| 3 |
A、4
| ||
B、8
| ||
C、12
| ||
D、36
|
在数列{an}中,a1=14,3an=3an+1+2,则使anan+2<0成立的n值是( )
| A、19 | B、20 | C、21 | D、22 |
若θ为三角形的一个内角,且sinθ+cosθ=
,则曲线 x2sinθ+y2cosθ=1是( )
| 1 |
| 5 |
| A、焦点在x轴上的双曲线 |
| B、焦点在y轴上的双曲线 |
| C、焦点在x轴上的椭圆 |
| D、焦点在y轴上的椭圆 |
要得到函数y=8(
)x的图象,可以把函数y=(
)x的图象( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、向右平移3个单位 |
| B、向左平移3个单位 |
| C、向右平移8个单位 |
| D、向左平移8个单位 |