题目内容
已知双曲线C:y2-
=1,过点P(2,1)作直线l交双曲线C于A、B两点.若P恰为弦AB的中点,则直线l的方程为 .
| x2 |
| 3 |
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:设A(x1,y1),B(x2,y2),则x1+x2=4,y1+y2=2,把A(x1,y1),B(x2,y2)代入双曲线C:y2-
=1,利用点差法求解.
| x2 |
| 3 |
解答:
解:设A(x1,y1),B(x2,y2),
∵P(2,1)恰为弦AB的中点,
∴x1+x2=4,y1+y2=2,
把A(x1,y1),B(x2,y2)代入双曲线C:y2-
=1,
得
,
两式相减,得:3(y1+y2)(y1-y2)-(x1+x2)(x1-x2)=0,
∴6(y1-y2)-4(x1-x2)=0,
∴k=
=
,
∴直线l的方程为y-1=
(x-2),
整理,得2x-3y-1=0.
故答案为:2x-3y-1=0.
∵P(2,1)恰为弦AB的中点,
∴x1+x2=4,y1+y2=2,
把A(x1,y1),B(x2,y2)代入双曲线C:y2-
| x2 |
| 3 |
得
|
两式相减,得:3(y1+y2)(y1-y2)-(x1+x2)(x1-x2)=0,
∴6(y1-y2)-4(x1-x2)=0,
∴k=
| y1-y2 |
| x1-x2 |
| 2 |
| 3 |
∴直线l的方程为y-1=
| 2 |
| 3 |
整理,得2x-3y-1=0.
故答案为:2x-3y-1=0.
点评:本题考查直线方程的求法,是中档题,解题时要认真审题,注意点差法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列{an}是等差数列,满足a2=5,a4=13.数列{bn}的前n项和是Tn,且Tn+bn=3.
(1)求数列{an}及数列{bn}的通项公式;
(2)若cn=an•bn,求数列{cn}中的最大项.
(1)求数列{an}及数列{bn}的通项公式;
(2)若cn=an•bn,求数列{cn}中的最大项.
在数列{an}中,a1=14,3an=3an+1+2,则使anan+2<0成立的n值是( )
| A、19 | B、20 | C、21 | D、22 |
若θ为三角形的一个内角,且sinθ+cosθ=
,则曲线 x2sinθ+y2cosθ=1是( )
| 1 |
| 5 |
| A、焦点在x轴上的双曲线 |
| B、焦点在y轴上的双曲线 |
| C、焦点在x轴上的椭圆 |
| D、焦点在y轴上的椭圆 |
下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,则能得出AB∥平面MNP的图形个数是( )
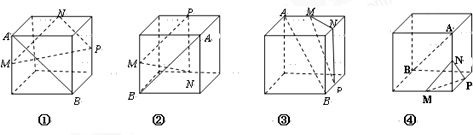

| A、1个 | B、2个 | C、3个 | D、4个 |
下列函数f(x)中,在(0,+∞)上为增函数的是( )
A、f(x)=
| ||
| B、f(x)=(x-1)2 | ||
| C、f(x)=lnx | ||
D、f(x)=(
|