题目内容
已知函数f(x)=ax2-ex(a∈R)
(Ⅰ)当a=1时,令h(x)=f′(x),求h(x)的单调区间;
(Ⅱ)若f(x)有两个极值点x1,x2(x1<x2).
(ⅰ)求实数a的取值范围;
(ⅱ)证明:-
<f(x1)<-1(注:e是自然对数的底数)
(Ⅰ)当a=1时,令h(x)=f′(x),求h(x)的单调区间;
(Ⅱ)若f(x)有两个极值点x1,x2(x1<x2).
(ⅰ)求实数a的取值范围;
(ⅱ)证明:-
| e |
| 2 |
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)当a=1时,直接求出h(x)=f′(x),利用导函数的符号,求h(x)的单调区间;
(Ⅱ)(ⅰ)若f(x)有两个极值点x1,x2(x1<x2).说明导函数为0,有两个解,利用函数的单调性,推出2a>φ(1)=e,求实数a的取值范围;
(ⅱ)由f'(x1)=0,推出a=
,x1∈(0,1),f(x1)=ax12-ex1=
•x12-ex1=ex1(
-1),构造函数φ(t)=et(
-1)(0<t<1),求出新函数的导数,φ(t)在0<t<1上单调递减,得到φ(1)<φ(t)<φ(0),即可证明:-
<f(x1)<-1.
(Ⅱ)(ⅰ)若f(x)有两个极值点x1,x2(x1<x2).说明导函数为0,有两个解,利用函数的单调性,推出2a>φ(1)=e,求实数a的取值范围;
(ⅱ)由f'(x1)=0,推出a=
| ex1 |
| 2x1 |
| ex1 |
| 2x1 |
| x1 |
| 2 |
| t |
| 2 |
| e |
| 2 |
解答:
解:(Ⅰ)当a=1时,h'(x)=2-ex,令h'(x)=0⇒x=ln2,---------(2分)
当x>ln2,h'(x)<0;x<ln2,h'(x)>0;
∴h'(x)的单调增区间为(-∞,ln2),单调减区间为(ln2,+∞)-------(5分)
(Ⅱ)(ⅰ)若f(x)有两个极值点x1,x2,则x1,x2是方程f'(x)=0的两个根,
故方程2ax-ex=0有两个根x1,x2,
又x=0显然不是该方程的根,∴方程2a=
有两个根,------(6分)
设φ(x)=
,得φ′=
,
当x<0时,φ(x)<0且φ'(x)<0,φ(x)单调递减,
当x>0时,φ(x)>0,当0<x<1时,φ'(x)<0,φ(x)单调递减;
当x>1时,φ'(x)>0,φ(x)单调递增,---------(9分)
要使方程2a=
有两个根,需2a>φ(1)=e,
故a>
且0<x1<1<x2,
故a的取值范围为(
,+∞)-------(10分)
(ⅱ)由f'(x1)=0,得2ax1-ex1=0,故a=
,x1∈(0,1)f(x1)=ax12-ex1=
•x12-ex1=ex1(
-1),x1∈(0,1)-----(12分)
设φ(t)=et(
-1)(0<t<1),则φ′(t)=et
<0,φ(t)在0<t<1上单调递减,
故φ(1)<φ(t)<φ(0),即-
<f(x1)<-1-------(14分)
当x>ln2,h'(x)<0;x<ln2,h'(x)>0;
∴h'(x)的单调增区间为(-∞,ln2),单调减区间为(ln2,+∞)-------(5分)
(Ⅱ)(ⅰ)若f(x)有两个极值点x1,x2,则x1,x2是方程f'(x)=0的两个根,
故方程2ax-ex=0有两个根x1,x2,
又x=0显然不是该方程的根,∴方程2a=
| ex |
| x |
设φ(x)=
| ex |
| x |
| ex(x-1) |
| x2 |
当x<0时,φ(x)<0且φ'(x)<0,φ(x)单调递减,
当x>0时,φ(x)>0,当0<x<1时,φ'(x)<0,φ(x)单调递减;
当x>1时,φ'(x)>0,φ(x)单调递增,---------(9分)
要使方程2a=
| ex |
| x |
故a>
| e |
| 2 |
故a的取值范围为(
| e |
| 2 |
(ⅱ)由f'(x1)=0,得2ax1-ex1=0,故a=
| ex1 |
| 2x1 |
| ex1 |
| 2x1 |
| x1 |
| 2 |
设φ(t)=et(
| t |
| 2 |
| t-1 |
| 2 |
故φ(1)<φ(t)<φ(0),即-
| e |
| 2 |
点评:本题考查函数的导数的综合应用,函数的单调性以及函数的极值,构造法二次求导的应用,综合性强.

练习册系列答案
相关题目
函数y=sin(-2x+
)在区间[0,π]上的单调递增区间为( )
| π |
| 3 |
A、[
| ||||
B、[0,
| ||||
C、[
| ||||
D、[
|
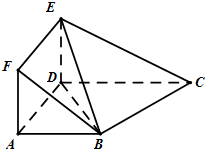 如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,
如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,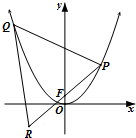 已知抛物线C:y=ax2,直线y=x+
已知抛物线C:y=ax2,直线y=x+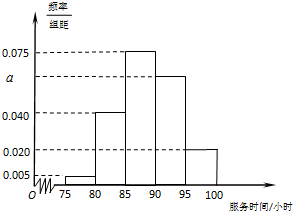 某市规定,高三毕业生三年在校期间参加不少于80小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据为样本,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.
某市规定,高三毕业生三年在校期间参加不少于80小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据为样本,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.