题目内容
已知F1，F2为双曲线
-
=1（a＞0，b＞0）的左右焦点，M为此双曲线上的一点，满足|MF1|=3|MF2|，那么此双曲线的离心率的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、（1，2） |
| B、（1，2] |
| C、（0，2） |
| D、[2，+∞） |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据|MF1|=3|MF2|，利用双曲线的定义，结合|MF1|+|MF2|=4|MF2|≥2c，即可求出双曲线的离心率的取值范围．
解答：
解：由题意，∵|MF1|=3|MF2|，
∴|MF1|-|MF2|=2|MF2|=2a，|MF1|+|MF2|=4|MF2|≥2c，
∴4a≥2c，
∴e≤2，
∵e＞1，
∴1＜e≤2．
故选：B．
∴|MF1|-|MF2|=2|MF2|=2a，|MF1|+|MF2|=4|MF2|≥2c，
∴4a≥2c，
∴e≤2，
∵e＞1，
∴1＜e≤2．
故选：B．
点评：本题考查双曲线离心率的计算问题．在求双曲线的离心率时，其关键是求出c，a之间的关系，即可求出双曲线的离心率，属于基础题．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
若复数z满足iz=2+4i，则在复平面内，z的共轭复数
对应的点的坐标是（ ）
. |
| z |
| A、（2，4） |
| B、（2，-4） |
| C、（4，-2） |
| D、（4，2） |
已知函数f（x）满足f（x+1）=
+f（x）（x∈R），且f（1）=
，则数列{f（n）}（n∈N*）前20项的和为（ ）
| 3 |
| 2 |
| 5 |
| 2 |
| A、305 | B、315 |
| C、325 | D、335 |
函数y=sin（-2x+
）在区间[0，π]上的单调递增区间为（ ）
| π |
| 3 |
A、[
| ||||
B、[0，
| ||||
C、[
| ||||
D、[
|
如果执行如图的程序框图，那么输出的S=
，那么判断框内是（ ）
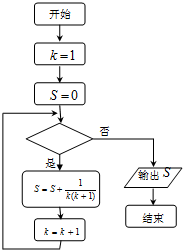
| 2013 |
| 2014 |
| A、k≤2013？ |
| B、k≤2014？ |
| C、k≥2013？ |
| D、k≥2014？ |
已知函数f（x）=ex-2x+a有零点，则实数a的取值范围是（ ）
| A、（-∞，2ln2-2] |
| B、[2ln2-2，+∞） |
| C、[2ln2，+∞） |
| D、[2ln2-2，2ln2] |
已知动点P的x坐标恒为0，y坐标恒为2，则动点P的轨迹是（ ）
| A、平面 | B、直线 |
| C、不是平面也不是直线 | D、以上都不对 |