题目内容
不等式组
（a为常数）表示的平面区域面积为81，则x2+y的最小值为 ．
|
考点：简单线性规划
专题：函数的性质及应用
分析：先根据平面区域的面积是81，求出a的值，从而求出x2+y的最小值．
解答：
解：画出满足条件的平面区域，
如图示：
，
∴S=a2=81，∴a=9，
令z=x2+y，则y=-x2+z，
∴当y=-x2+z过（9，-9）时，z取到最小值，
z最小值=72，
故答案为：72．
如图示：
，∴S=a2=81，∴a=9，
令z=x2+y，则y=-x2+z，
∴当y=-x2+z过（9，-9）时，z取到最小值，
z最小值=72，
故答案为：72．
点评：本题考查了线性规划问题，考查了数形结合思想，是一道中档题．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
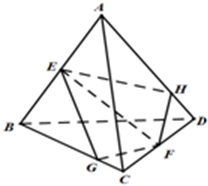如图，在四面体ABCD中，E，F分别为AB，CD的中点，过EF任作一个平面α分别与直线BC，AD相交于点G，H，下列判断中：