题目内容
已知函数f(x)=a•4x-2x+1-a.
(1)若a=0,解方程f(2x)=-4;
(2)若函数f(x)=a•4x-2x+1-a在[1,2]上有零点,求实数a的取值范围.
(1)若a=0,解方程f(2x)=-4;
(2)若函数f(x)=a•4x-2x+1-a在[1,2]上有零点,求实数a的取值范围.
考点:函数零点的判定定理,函数的零点
专题:计算题,函数的性质及应用
分析:(1)代入a=0,从而求解方程;
(2)令t=2x,x∈[1,2],则t∈[2,4];a=
=
,令g(t)=t-
,从而求解a.
(2)令t=2x,x∈[1,2],则t∈[2,4];a=
| 2t |
| t2-1 |
| 2 | ||
t-
|
| 1 |
| t |
解答:
解:(1)由题意,f(2x)=-22x+1=-4,
解得,x=
.
(2)令t=2x,x∈[1,2],则t∈[2,4];
由题意,at2-2t-1=0在[2,4]上有零点,
a=
=
,令g(t)=t-
,
则g(t)在[2,4]上为增函数.
则g(t)∈[
,
],从而a∈[
,
].
解得,x=
| 1 |
| 2 |
(2)令t=2x,x∈[1,2],则t∈[2,4];
由题意,at2-2t-1=0在[2,4]上有零点,
a=
| 2t |
| t2-1 |
| 2 | ||
t-
|
| 1 |
| t |
则g(t)在[2,4]上为增函数.
则g(t)∈[
| 3 |
| 2 |
| 15 |
| 4 |
| 8 |
| 15 |
| 4 |
| 3 |
点评:本题考查了函数的零点的解法,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知等比数列{an}前n项的积为Tn,且公比q≠1,若T7=128,则( )
| A、a4=2 |
| B、a5=2 |
| C、a6=2 |
| D、a1=2 |
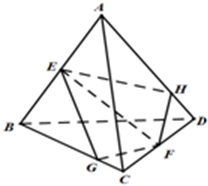 如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面α分别与直线BC,AD相交于点G,H,下列判断中:
如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面α分别与直线BC,AD相交于点G,H,下列判断中: