题目内容
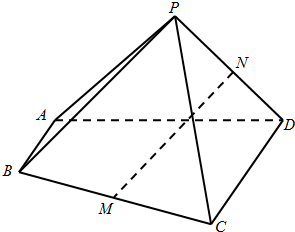 如图,四棱锥P-ABCD中,AB∥CD,AB⊥AD,BC=CD=2AB=2,△PAD是等边三角形,M、N分别为BC、PD的中点.
如图,四棱锥P-ABCD中,AB∥CD,AB⊥AD,BC=CD=2AB=2,△PAD是等边三角形,M、N分别为BC、PD的中点.(1)求证:MN∥平面PAB;
(2)若MN⊥PD,求二面角P-AD-C的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)取PC中点Q,可证面NQM∥面PAB,得MN∥面PAB;
(2)取AD中点O,PO⊥AD,MO⊥AD,∠POM是二面角P-AD-C平面角,解三角形得二面角P-AD-C的余弦值.
(2)取AD中点O,PO⊥AD,MO⊥AD,∠POM是二面角P-AD-C平面角,解三角形得二面角P-AD-C的余弦值.
解答:
证明:(1)取PC中点Q,连接QN,QM,如下图所示:

∵M、N分别为BC、PD的中点.
∴QM∥PB,
又∵QM?平面PAB,PB?平面PAB,
∴QM∥平面PAB,
同理QN∥平面PAB,
∵QM∩QN=Q,QM,QN?平面NQM
∴平面NQM∥平面PAB,
又∵MN?平面NQM
∴MN∥面PAB;
解:(2)取AD中点O,连接OP,OM,

∵△PAD是等边三角形,
∴PO⊥AD,
∵AB∥CD,AB⊥AD,
∴MO⊥AD,
∴∠POM是二面角P-AD-C平面角,
∵BC=CD=2AB=2,
∴AD=
,MB=MC=1,∠BCD=
,
∴MD=
,PO=
×
=
,
又∵MN⊥PD,
∴PM=MD=
,MO=
,
由余弦定理得:cos∠POM=
.
故二面角P-AD-C的余弦值为

∵M、N分别为BC、PD的中点.
∴QM∥PB,
又∵QM?平面PAB,PB?平面PAB,
∴QM∥平面PAB,
同理QN∥平面PAB,
∵QM∩QN=Q,QM,QN?平面NQM
∴平面NQM∥平面PAB,
又∵MN?平面NQM
∴MN∥面PAB;
解:(2)取AD中点O,连接OP,OM,

∵△PAD是等边三角形,
∴PO⊥AD,
∵AB∥CD,AB⊥AD,
∴MO⊥AD,
∴∠POM是二面角P-AD-C平面角,
∵BC=CD=2AB=2,
∴AD=
| 3 |
| π |
| 3 |
∴MD=
| 3 |
| ||
| 2 |
| 3 |
| 3 |
| 2 |
又∵MN⊥PD,
∴PM=MD=
| 3 |
| 3 |
| 2 |
由余弦定理得:cos∠POM=
| 1 |
| 3 |
故二面角P-AD-C的余弦值为
| 1 |
| 3 |
点评:本题考查的知识点是二面角的平面角及求法,直线与平面平行的判定,平面与平面平行的判定与性质,难度中档.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
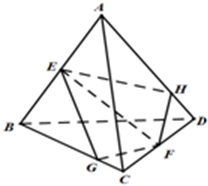 如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面α分别与直线BC,AD相交于点G,H,下列判断中:
如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面α分别与直线BC,AD相交于点G,H,下列判断中: