题目内容

某船在A处看测得一个灯塔B在北偏东60°方向，之后该船以每小时15
2
km的速度向正东方向航行，行驶4小时后到达C处，在C处测得灯塔B在北偏东15°方向，此时该船与灯塔B的距离为
 
km．
考点：解三角形的实际应用
专题：应用题,解三角形
分析：由题意，AC=60
2
km，∠BAC=30°，∠ACB=105°，∠B=45°，由正弦定理可得BC．
解答： 解：由题意，AC=60
2
km，∠BAC=30°，∠ACB=105°，
∴∠B=45°，
由正弦定理可得：
60
2
sin45°
=
BC
sin30°

∴BC=60．
故答案为：60．
点评：本题考查解三角形的实际应用，考查正弦定理的运用，比较基础．
练习册系列答案
相关题目
定义在D上的函数f（x），如果满足：对任意x∈D，存在常数M≥0，都有|f（x）|≤M成立，则称f（x）是D上的有界函数，其中M称为函数f（x）的一个上界．已知函数f(x)=1+a(
1
2
)x+(
1
4
)x，g(x)=log
1
2
1-ax
x-1
．
（1）若函数g（x）为奇函数，求实数a的值；
（2）若a=-1，判断g（x）在区间[
5
3
，3]上的单调性（不必证明），并求g（x）上界的最小值；
（3）若函数f（x）在[0，+∞）上是以3为上界的有界函数，求实数a的取值范围．
设复数z满足（1+2i）z=4+3i．
（Ⅰ）求复数
.
z
；
（Ⅱ）当
2
3
＜m＜1时，试判断复数m（3+i）-
.
z
在复平面内对应的点位于哪个象限？写出推理过程．
已知函数f（x）=Asin（ωx+φ）（A＞0，ω，0，|φ|＜π），在同一周期内，当x=
π
12
时，f（x）取得最大值3；当x=
7
12
π时，f（x）取得最小值-3．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）若x∈[-
π
3
，
π
6
]时，函数h（x）=2f（x）+1-m有两个零点，求实数m的取值范围．
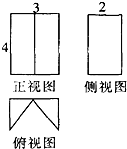如图，是一个几何体的正视图、侧视图、俯视图，且正视图、侧视图都是矩形，则该几何体的体积是
 
．
已知
a
=（1，2），
b
=（-2，k），若
a
∥（
a
+
b
），则实数k的值为
 
．
已知f（x+1）=x2-2x，则f（2）=
 
．
考察下列一组不等式：23+53＞22.5+2.55，24+54＞23.5+2.53，24+54＞23.5+2.53，25+55＞23.52+22.53，+…+
将上述不等式在左右两端仍为两项和的情况下加以推广，使以上的不等式成为推广不等式的特例，则推广的不等式可以是
 
．
若关于x的不等式|ax-1|≤3的解集为{x|-1≤x≤
1
2
}，则a=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网