题目内容
定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M≥0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的一个上界.已知函数f(x)=1+a(
)x+(
)x,g(x)=log
.
(1)若函数g(x)为奇函数,求实数a的值;
(2)若a=-1,判断g(x)在区间[
,3]上的单调性(不必证明),并求g(x)上界的最小值;
(3)若函数f(x)在[0,+∞)上是以3为上界的有界函数,求实数a的取值范围.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1-ax |
| x-1 |
(1)若函数g(x)为奇函数,求实数a的值;
(2)若a=-1,判断g(x)在区间[
| 5 |
| 3 |
(3)若函数f(x)在[0,+∞)上是以3为上界的有界函数,求实数a的取值范围.
考点:函数的值域
专题:函数的性质及应用
分析:(1)由g(x)为奇函数,得:
=
,解出即可;
(2)由(1)得:g(x)=
,根据函数的单调性,故函数g(x)在区间[
,3]上的上界的最小值为2.
(3)由题意知,|f(x)|≤3在[0,+∞)上恒成立.P(t1)-p(t2)=
<0,得h(t)在[1,+∞)上递减,显然p(t)在[1,+∞)上递增,从而求出a的范围.
| 1+ax |
| -x-1 |
| x-1 |
| 1-ax |
(2)由(1)得:g(x)=
| log |
|
| 5 |
| 3 |
(3)由题意知,|f(x)|≤3在[0,+∞)上恒成立.P(t1)-p(t2)=
| (t1-t2)(2t1t2+1) |
| t1t2 |
解答:
解:(1)因为函数g(x)为奇函数,
所以g(-x)=-g(x)即:
=
,
得a=±1,而当a=1时不合题意,
故a=-1;
(2)由(1)得:g(x)=
,
函数g(x)在区间(1,+∞)上单调递增,
所以函数g(x)在区间[
,3]上单调递增,
函数g(x)在区间[
,3]上的值域为[-2,-1],
所以|g(x)|≤2,故函数g(x)在区间[
,3]上的上界的最小值为2.
(3)由题意知,|f(x)|≤3在[0,+∞)上恒成立.
-3≤f(x)≤3,-4-(
)x≤a(
)x≤2-(
)x.
∴[-4•2x-(
)x]max≤a≤[2•2x-(
)x]min,
设2x=t,h(t)=-4t-
,p(t)=2t-
,
由x∈[0,+∞)得 t≥1,
设1≤t1<t2,h(t1)-h(t2)=
>0,
P(t1)-p(t2)=
<0,
所以h(t)在[1,+∞)上递减,显然p(t)在[1,+∞)上递增,
h(t)在[1,+∞)上的最大值为h(1)=-5,
p(t)在[1,+∞)上的最小值为p(1)=1.
所以实数a的取值范围为[-5,1].
所以g(-x)=-g(x)即:
| 1+ax |
| -x-1 |
| x-1 |
| 1-ax |
得a=±1,而当a=1时不合题意,
故a=-1;
(2)由(1)得:g(x)=
| log |
|
函数g(x)在区间(1,+∞)上单调递增,
所以函数g(x)在区间[
| 5 |
| 3 |
函数g(x)在区间[
| 5 |
| 3 |
所以|g(x)|≤2,故函数g(x)在区间[
| 5 |
| 3 |
(3)由题意知,|f(x)|≤3在[0,+∞)上恒成立.
-3≤f(x)≤3,-4-(
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴[-4•2x-(
| 1 |
| 2 |
| 1 |
| 2 |
设2x=t,h(t)=-4t-
| 1 |
| t |
| 1 |
| t |
由x∈[0,+∞)得 t≥1,
设1≤t1<t2,h(t1)-h(t2)=
| (t1-t2)(4t1t2-1) |
| t1t2 |
P(t1)-p(t2)=
| (t1-t2)(2t1t2+1) |
| t1t2 |
所以h(t)在[1,+∞)上递减,显然p(t)在[1,+∞)上递增,
h(t)在[1,+∞)上的最大值为h(1)=-5,
p(t)在[1,+∞)上的最小值为p(1)=1.
所以实数a的取值范围为[-5,1].
点评:本题考查了函数的值域问题,函数的最值问题,考查了新定义问题,本题属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
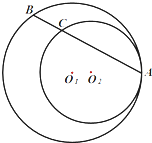 如图,圆O1与圆O2内切于点A,其半径分别为r1与r2(r1>r2),圆O1的弦AB交圆O2于点C(O1不在AB上),求证:AB:AC为定值.
如图,圆O1与圆O2内切于点A,其半径分别为r1与r2(r1>r2),圆O1的弦AB交圆O2于点C(O1不在AB上),求证:AB:AC为定值.