题目内容
已知
=（1，2），
=（-2，k），若
∥（
+
），则实数k的值为 ．
| a |
| b |
| a |
| a |
| b |
考点：平面向量共线（平行）的坐标表示
专题：平面向量及应用
分析：由向量加法的坐标运算求得
+
=(-1，2+k)，然后直接利用向量共线的坐标表示列式求解．
| a |
| b |
解答：
解：由
=（1，2），
=（-2，k），得
+
=(-1，2+k)，
∵
∥（
+
），
∴1×（2+k）-2×（-1）=0，
解得：k=-4．
故答案为：-4
| a |
| b |
| a |
| b |
∵
| a |
| a |
| b |
∴1×（2+k）-2×（-1）=0，
解得：k=-4．
故答案为：-4
点评：平行问题是一个重要的知识点，在高考题中常常出现，常与向量的模、向量的坐标表示等联系在一起，要特别注意垂直与平行的区别．若
=（a1，a2），
=（b1，b2），则
⊥
?a1a2+b1b2=0，
∥
?a1b2-a2b1=0，是基础题．
| a |
| b |
| a |
| b |
| a |
| b |
练习册系列答案
名校课堂系列答案
相关题目
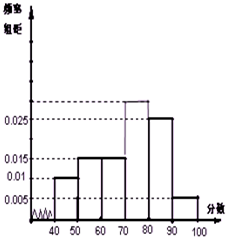某校从参加高一年级期末考试的学生中抽出60名学生，将其某科成绩（是不小于40不大于100的整数）分成六段[40，50），[50，60）…[90，100]后画出如下频率分布直方图，根据图形中所给的信息，回答以下问题：
