题目内容
已知f（x+1）=x2-2x，则f（2）= ．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：首先，换元令x+1=t，得到x=t-1，然后，得到函数解析式，然后，求解f（2）的值即可．
解答：
解：令x+1=t，
∴x=t-1，
∴f（t）=（t-1）2-2（t-1）=t2-4t+3，
∴f（x）=x2-4x+3，
∴f（2）=-1
故答案为：-1
∴x=t-1，
∴f（t）=（t-1）2-2（t-1）=t2-4t+3，
∴f（x）=x2-4x+3，
∴f（2）=-1
故答案为：-1
点评：本题重点考查了函数的换元法求解函数解析式，注意运用此方法时，容易出现变量的范围扩大或者缩小等问题，需要引起足够重视，属于基础题．
练习册系列答案
相关题目
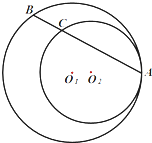如图，圆O1与圆O2内切于点A，其半径分别为r1与r2（r1＞r2），圆O1的弦AB交圆O2于点C（O1不在AB上），求证：AB：AC为定值．
