题目内容
设复数z满足(1+2i)z=4+3i.
(Ⅰ)求复数
;
(Ⅱ)当
<m<1时,试判断复数m(3+i)-
在复平面内对应的点位于哪个象限?写出推理过程.
(Ⅰ)求复数
. |
| z |
(Ⅱ)当
| 2 |
| 3 |
. |
| z |
考点:复数代数形式的乘除运算,复数的代数表示法及其几何意义
专题:数系的扩充和复数
分析:(Ⅰ)把给出的等式变形,然后利用复数代数形式的乘除运算化简求得z,则
可求;
(Ⅱ)把
代入m(3+i)-
,整理后结合m的范围得答案.
. |
| z |
(Ⅱ)把
. |
| z |
. |
| z |
解答:
解:(Ⅰ)∵(1+2i)z=4+3i,
∴z=
=
=
=2-i,
∴
=2+i;
(Ⅱ)m(3+i)-
=m(3+i)-(2+i)=(3m-2)+(m-1)i,
∵
<m<1,
∴3m-2>0,m-1<0.
∴复数m(3+i)-
在复平面内对应的点位于第四象限.
∴z=
| 4+3i |
| 1+2i |
| (4+3i)(1-2i) |
| (1+2i)(1-2i) |
| 10-5i |
| 5 |
∴
. |
| z |
(Ⅱ)m(3+i)-
. |
| z |
∵
| 2 |
| 3 |
∴3m-2>0,m-1<0.
∴复数m(3+i)-
. |
| z |
点评:本题考查了复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
相关题目
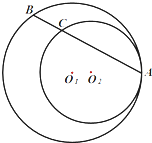 如图,圆O1与圆O2内切于点A,其半径分别为r1与r2(r1>r2),圆O1的弦AB交圆O2于点C(O1不在AB上),求证:AB:AC为定值.
如图,圆O1与圆O2内切于点A,其半径分别为r1与r2(r1>r2),圆O1的弦AB交圆O2于点C(O1不在AB上),求证:AB:AC为定值.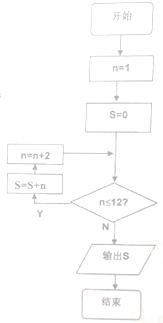 阅读如图程序框图,
阅读如图程序框图,