题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,ω,0,|φ|<π),在同一周期内,当x=
时,f(x)取得最大值3;当x=
π时,f(x)取得最小值-3.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若x∈[-
,
]时,函数h(x)=2f(x)+1-m有两个零点,求实数m的取值范围.
| π |
| 12 |
| 7 |
| 12 |
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若x∈[-
| π |
| 3 |
| π |
| 6 |
考点:三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)已知函数f(x)=Asin(ωx+φ)(A>0,ω,0,|φ|<π),在同一周期内,当x=
时,f(x)取得最大值3;当x=
π时,f(x)取得最小值-3.所以确定A=3,又由于在一个周期内最大值与最小值之间的距离正好是半个周期从而求得ω,进一步根据最值确定φ.
(2)根据自变量的范围,确定函数的零点,即求h(x)=0的根,进一步求出实数m的取值范围.
| π |
| 12 |
| 7 |
| 12 |
(2)根据自变量的范围,确定函数的零点,即求h(x)=0的根,进一步求出实数m的取值范围.
解答:
解:(1)∵f(x)=Asin(ωx+φ)(A>0,ω,0,|φ|<π),在同一周期内,当x=
时,f(x)取得最大值3;
当x=
π时,f(x)取得最小值-3.
∴A=3
=
-
=
∴T=π
∵ω=
∴ω=2
又∵函数在同一周期内,当x=
时,f(x)取得最大值3.
∴2×
+φ=
+2kπ (k∈Z)
解得 φ=2kπ+
(k∈Z)
又∵|φ|<π
∴φ=
进一步求得:f(x)=3sin(2x+
)
(2)∵在x∈[-
,
]时,函数h(x)=2f(x)+1-m有两个零点
∴h(x)=0有两个实数根,即函数图象有两个交点.
∴sin(2x+
)=
在[-
,
]上有两个根
∵x∈[-
,
]
∴2x+
∈[-
,
]
∴
∈[
,1)
即m∈[3
+1,7).
| π |
| 12 |
当x=
| 7 |
| 12 |
∴A=3
| T |
| 2 |
| 7π |
| 12 |
| π |
| 12 |
| π |
| 2 |
∴T=π
∵ω=
| 2π |
| T |
∴ω=2
又∵函数在同一周期内,当x=
| π |
| 12 |
∴2×
| π |
| 12 |
| π |
| 2 |
解得 φ=2kπ+
| π |
| 3 |
又∵|φ|<π
∴φ=
| π |
| 3 |
进一步求得:f(x)=3sin(2x+
| π |
| 3 |
(2)∵在x∈[-
| π |
| 3 |
| π |
| 6 |
∴h(x)=0有两个实数根,即函数图象有两个交点.
∴sin(2x+
| π |
| 3 |
| m-1 |
| 6 |
| π |
| 3 |
| π |
| 6 |
∵x∈[-
| π |
| 3 |
| π |
| 6 |
∴2x+
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴
| m-1 |
| 6 |
| ||
| 2 |
即m∈[3
| 3 |
点评:本题重点考查知识点:三角函数的解析式的求法,以及在某一定义域下利用函数的零点求参数的取值范围问题.是很好的高考题型.

练习册系列答案
相关题目
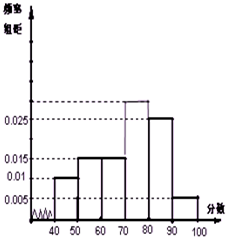 某校从参加高一年级期末考试的学生中抽出60名学生,将其某科成绩(是不小于40不大于100的整数)分成六段[40,50),[50,60)…[90,100]后画出如下频率分布直方图,根据图形中所给的信息,回答以下问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其某科成绩(是不小于40不大于100的整数)分成六段[40,50),[50,60)…[90,100]后画出如下频率分布直方图,根据图形中所给的信息,回答以下问题: