题目内容
已知函数f(x)=kx,g(x)=
(Ⅰ)求函数g(x)=
的单调区间;
(Ⅱ)若不等式f(x)≥g(x)在区间(0,+∞)上恒成立,求实数k的取值范围;
(Ⅲ)求证
+
+…+
<
.
| 1nx |
| x |
(Ⅰ)求函数g(x)=
| 1nx |
| x |
(Ⅱ)若不等式f(x)≥g(x)在区间(0,+∞)上恒成立,求实数k的取值范围;
(Ⅲ)求证
| 1n2 | ||
|
| 1n3 | ||
|
| 1nn | ||
|
| 1 |
| 2e |
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(Ⅰ)先求导,根据导数求出函数的单调区间.
(Ⅱ)分离参数,再构造函数h(x)=
,再求导,利用导数求出函数的最值.
(Ⅲ)由(Ⅱ)知
≤
,即
≤
•
(x≥2),利用放缩法,证明即可.
(Ⅱ)分离参数,再构造函数h(x)=
| lnx |
| x2 |
(Ⅲ)由(Ⅱ)知
| lnx |
| x2 |
| 1 |
| 2e |
| lnx |
| x4 |
| 1 |
| 2e |
| 1 |
| x2 |
解答:
解:(Ⅰ)∵g(x)=
,x>0,故其定义域为(0,+∞)
∴g′(x)=
,
令g′(x)>0,得0<x<e
令g′(x)<0,得x>e
故函数的单调递增区间为(0,e),单调递减区间为(e,+∞).
(Ⅱ)∵x>0,kx≥
∴k≥
,
令h(x)=
,
∴h′(x)=
令h′(x)=0,解得x=
,
当x在(0,+∞)内变化时,h′(x),h(x)变化如下表
由表知,当时函数h(x)有最大值,且最大值为
,
所以实数k的取值范围[
,+∞)
(Ⅲ),由(Ⅱ)知
≤
,
∴
≤
•
(x≥2),
∴
+
+…+
<
(
+
+…+
)<
(
+
+…+
)=
[(1-
)+(
-
)+…+(
-
)]=
(1-
)<
| 1nx |
| x |
∴g′(x)=
| 1-lnx |
| x2 |
令g′(x)>0,得0<x<e
令g′(x)<0,得x>e
故函数的单调递增区间为(0,e),单调递减区间为(e,+∞).
(Ⅱ)∵x>0,kx≥
| 1nx |
| x |
∴k≥
| lnx |
| x2 |
令h(x)=
| lnx |
| x2 |
∴h′(x)=
| 1-2lnx |
| x3 |
令h′(x)=0,解得x=
| e |
当x在(0,+∞)内变化时,h′(x),h(x)变化如下表
| x | (0,
|
| (
| ||||||
| h′(x) | + | 0 | - | ||||||
| h(x) | ↗ |
| ↘ |
| 1 |
| 2e |
所以实数k的取值范围[
| 1 |
| 2e |
(Ⅲ),由(Ⅱ)知
| lnx |
| x2 |
| 1 |
| 2e |
∴
| lnx |
| x4 |
| 1 |
| 2e |
| 1 |
| x2 |
∴
| 1n2 | ||
|
| 1n3 | ||
|
| 1nn | ||
|
| 1 |
| 2e |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 1 |
| 2e |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| (n-1)n |
| 1 |
| 2e |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| 2e |
| 1 |
| n |
| 1 |
| 2e |
点评:本题考查利用导数求闭区间上函数的最值的应用以及利用放缩法证明不等式,考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
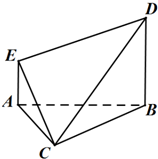 如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1.
如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1.