Question

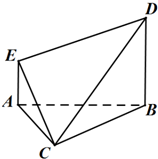如图，在多面体ABCDE中，AE⊥平面ABC，BD∥AE，且AC=AB=BC=BD=2，AE=1．
（Ⅰ）求直线CE与平面BCD所成角的正弦值；  
（Ⅱ）求二面角C-DE-A的正切值．

Answer 1

考点：直线与平面所成的角,二面角的平面角及求法

专题：空间角

分析：（Ⅰ）以A为原点，AB为y轴，AE为z轴，建立空间直角坐标系，利用向量法能求出直线CE与平面BCD所成角的正弦值．
（Ⅱ）分别求出平面CED的法向量和平面ADE的法向量，利用向量法能求出二面角C-DE-A的正切值．

解答： 解：（Ⅰ）以A为原点，AB为y轴，AE为z轴，
建立空间直角坐标系，
由已知得C（

3

，1，0），E（0，0，1），
B（0，2，0），D（0，2，2），

EC

=（

3

，1，-1），

BC

=（

3

，-1，0），

BD

=（0，0，2），
设平面BDC的法向量

n

=(x，y，z)，
则

n • BC = 3 x-y=0 n • BD =2z=0

，
取x=

3

，得

n

=（

3

，3，0），
设直线CE与平面BCD所成角为θ，
则sinθ=|cos＜

n

，

EC

＞|=|

3+3+0

5 • 12

|=

15

5

，
∴直线CE与平面BCD所成角的正弦值为

15

5

．
（Ⅱ）

EC

=（

3

，1，-1），

ED

=（0，2，1），
设平面CED的法向量

m

=（a，b，c），
则

m • EC = 3 a+b-c=0 m • ED =2b+c=0

，
取a=

3

，得

m

=（

3

，-1，2），
又平面ADE的法向量

p

=（1，0，0），
设二面角C-DE-A的平面角为θ，
cosθ=|cos＜

m

，

p

＞|=|

3

8

|=

6

4

，
∴tanθ=

15

3

．
∴二面角C-DE-A的正切值为

15

3

．

点评：本题考查直线与平面所成角的正弦值的求法，考查二面角的正切值的求法，是中档题，解题时要注意向量法的合理运用．