题目内容

过双曲线
x2
4
-
y2
8
=1的右焦点作一直线l交双曲线于A，B两点，若|AB|=8，则这样的直线l共有（　　）条？
A、1B、2C、3D、4
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：先看当A、B都在右支上时，若AB垂直x轴，根据双曲线方程求得焦点的坐标，把焦点横坐标代入双曲线方程求得交点的纵坐标，进而求得AB的长等于8，则即为垂直于x轴的一条；再看若A、B分别在两支先看A，B为两顶点时，不符合题意进而可推断出符合题意的直线有两条，最后综合可得答案．
解答： 解：①若A、B都在右支，
若AB垂直x轴，a2=4，b2=8，c2=12，所以F（2
3
，0）
则AB：x=2
3
，
代入双曲线
x2
4
-
y2
8
=1，求得y=±4，所以AB=|y1-y2|=8，
所以|AB|=8的有一条，即垂直于x轴；
②若A、B分别在两支
a=2，所以顶点距离为2+2=4＜8，所以|AB|=8有两条，关于x轴对称．
所以一共3条
故选C．
点评：本题主要考查了双曲线的对称性和直线与双曲线的关系．考查了学生分析推理和分类讨论思想的运用．
练习册系列答案
相关题目
已知函数y=f（x），对任意的两个不相等的实数x1，x2，都有f（x1+x2）=f（x1）•f（x2）成立，且f（0）≠0，则f（-5）•f（-3）•f（-1）•f（1）•f（3）•f（5）的值为
 
．
下列命题：
①三角形一定是平面图形；
②互相平行的三条直线都在同一平面内；
③梯形一定是平面图形；
④四边都相等的四边形是菱形．
其中真命题的个数是（　　）
A、1B、2C、3D、4
已知函数f（x）=kx，g（x）=
1nx
x

（Ⅰ）求函数g（x）=
1nx
x
的单调区间；
（Ⅱ）若不等式f（x）≥g（x）在区间（0，+∞）上恒成立，求实数k的取值范围；
（Ⅲ）求证
1n2
2
4
 
+
1n3
3
4
 
+…+
1nn
n
4
 
＜
1
2e
．
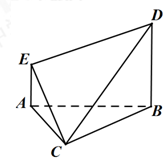如图，在多面体ABCDE中，AE⊥平面ABC，BD∥AE，且AC=AB=BC=BD=2，AE=1
（Ⅰ）求二面角C-BD-A的大小；  
（Ⅱ）求直线CE与平面BCD所成角的正弦值．
AB为过椭圆
x2
a2
+
y2
b2
=1中心的弦，F（c，0）为它的焦点，则△FAB的最大面积为（　　）
A、b2B、ab
C、acD、bc
已知公差不为0的等差数列{an}中，a1=2，{an}部分项按原来的顺序由小到大组成等比数列{akn}，且k1=1，k2=3，k3=11．
（1）求该等比数列的公比q；  
（2）求akn及kn．
已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)过点A(1，
2
2
)，且离心率为
2
2
．
（1）求椭圆的标准方程；
（2）过右焦点l：x=4的直线P与椭圆l相交于d两点，且
F1P
⊥
F1Q
，求直线C的方程．
已知函数f（x）=
1，x≥0
1-x2，x＜0
，则满足不等式f（1-x2）＞f（2x）的x的取值集合是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网