题目内容
已知三棱柱ABC-A1B1C1,底面ABC是边长为10的正三角形,侧棱AA1垂直于底面ABC,且AA1=12,过底面一边AB,作与底面ABC成60°角的截面面积是 .
考点:棱柱的结构特征
专题:空间位置关系与距离
分析:如图所示.过底面一边AB,作与底面ABC成60°角的截面为BCF1E1.利用截面的面积=
即可得出.
| S梯形BCFE |
| cos60° |
解答:
解:如图所示.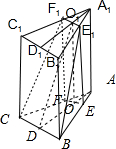
过底面一边AB,作与底面ABC成60°角的截面为BCF1E1.
作E1E⊥AB交AB于点E,作F1F⊥AC交AC于点F.
分别作底面ABC、A1B1C1的边BC、B1C1上的高,分别交EF、E1F1于点O、O1.
则O1O=A1A=12.
∵tan60°=
=
,解得OD=4
.
而AD=5
.
∴S梯形BCFE=
S△ABC=
×
×102=24
.
∴截面的面积=
=48
.
故答案为:48
.

过底面一边AB,作与底面ABC成60°角的截面为BCF1E1.
作E1E⊥AB交AB于点E,作F1F⊥AC交AC于点F.
分别作底面ABC、A1B1C1的边BC、B1C1上的高,分别交EF、E1F1于点O、O1.
则O1O=A1A=12.
∵tan60°=
| O1O |
| OD |
| 12 |
| OD |
| 3 |
而AD=5
| 3 |
∴S梯形BCFE=
| 24 |
| 25 |
| 24 |
| 25 |
| ||
| 4 |
| 3 |
∴截面的面积=
| S梯形BCFE |
| cos60° |
| 3 |
故答案为:48
| 3 |
点评:本题考查了二面角的平面角、截面与射影的面积之间的关系、直角三角形的边角关系,考查了空间想象能力,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知函数y=f(x),对任意的两个不相等的实数x1,x2,都有f(x1+x2)=f(x1)•f(x2)成立,且f(0)≠0,则f(-5)•f(-3)•f(-1)•f(1)•f(3)•f(5)的值为 .
f(x)=
是定义在(-∞,+∞)上是减函数,则a的取值范围是( )
|
A、[
| ||||
B、[0,
| ||||
C、(0,
| ||||
D、(-∞,
|
已知a2+b2+c2=1,若
a+
b+2c≤|x-1|+|x+m|对任意实数a,b,c,x恒成立,则实数m的取值范围是( )
| 2 |
| 3 |
| A、[8,+∞) |
| B、(-∞,-4]∪[2,+∞) |
| C、(-∞,-1]∪[8,+∞) |
| D、[2,+∞) |