题目内容
P（x，y）是椭圆
+
=1上的点，若m=2x-y，则m的取值范围是 ．
| x2 |
| 9 |
| y2 |
| 4 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由P（x，y）是椭圆
+
=1上的点，设x=3cosa，y=2sina，（0≤a≤2π），从而求解．
| x2 |
| 9 |
| y2 |
| 4 |
解答：
解：∵P（x，y）是椭圆
+
=1上的点，
∴设x=3cosa，y=2sina，（0≤a≤2π），
∴m=2x-y=6cosa-2sina
=2
sin（a+θ），
∵-1≤sin（a+θ）≤1，
∴-2
≤2
sin（a+θ）≤2
，
故答案为：[-2
，2
]．
| x2 |
| 9 |
| y2 |
| 4 |
∴设x=3cosa，y=2sina，（0≤a≤2π），
∴m=2x-y=6cosa-2sina
=2
| 10 |
∵-1≤sin（a+θ）≤1，
∴-2
| 10 |
| 10 |
| 10 |
故答案为：[-2
| 10 |
| 10 |
点评：本题考查了椭圆的简单性质，借助参数方程使化简简化，属于中档题．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
下列各组中的两个函数是同一函数的是（ ）
| A、f（x）=（x-1）0与g（x）=1 | ||||||||
B、f（x）=x与g（x）=
| ||||||||
C、f（x）=
| ||||||||
D、f（x）=
|
f（x）=
是定义在（-∞，+∞）上是减函数，则a的取值范围是（ ）
|
A、[
| ||||
B、[0，
| ||||
C、（0，
| ||||
D、（-∞，
|
点P为抛物线：y2=4x上一动点，定点A(2，4
)，则|PA|与P到y轴的距离之和的最小值为（ ）
| 5 |
| A、9 | B、10 | C、8 | D、5 |
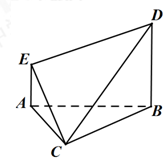如图，在多面体ABCDE中，AE⊥平面ABC，BD∥AE，且AC=AB=BC=BD=2，AE=1